MRTS
Marginal rate of technical substitution (MRTS) is the rate at which a firm can substitute capital with labor. It equals the change in capital to change in labor which in turn equals the ratio of marginal product of labor to marginal product of capital.
MRTS equals the slope of an isoquant. An isoquant is a curve which represents combinations of different factors of production i.e. labor and capital that yield the same total production.
The concept behind MRTS is similar to that of marginal rate of substitution (MRS). While the marginal rate of substitution tells us the rate at which a consumer is willing to replace one product with another, the marginal rate of technical substitution tells us the rate at which a producer is willing to switch one input (i.e. factor of production) with another. MRTS is relevant to producers and MRS is relevant to consumers.
Formula
Marginal rate of substitution can be worked out using the following formula:
$$ \mathrm{\text{MRTS}=}\frac{\mathrm{\text{Change in Capital}}}{\mathrm{\text{Change in Labor}}} $$
MRTS can also be worked out using the marginal product of labor and marginal product of capital as follows:
$$ \mathrm{\text{MRTS}=}\frac{{\mathrm{\text{MP}}} _ \mathrm{\text{L}}}{{\mathrm{\text{MP}}} _ \mathrm{\text{K}}} $$
Where MPL is the marginal product of labor and MPK is the marginal product of capital.
Marginal product of labor is the increase in total production that results from the incremental unit of labor. In other words, it equals the difference between the total product using n units of labor minus total product using n – 1 units of labor while keeping capital constant.
Marginal product of capital is the increase in total production that results from the marginal (i.e. the last) unit of capital while keeping labor and other inputs constant.
Example
The following table shows different units of capital (K) and labor (L) which a firm uses to produce 10 units
| Capital (K) | Labor (L) |
|---|---|
| 10.00 | 100.00 |
| 12.00 | 75.00 |
| 14.40 | 56.25 |
| 17.28 | 42.19 |
| 20.74 | 31.64 |
| 24.88 | 23.73 |
| 29.86 | 17.80 |
| 35.83 | 13.35 |
| 43.00 | 10.01 |
| 51.60 | 7.51 |
| 61.92 | 5.63 |
If we plot the data above, we get a convex isoquant.
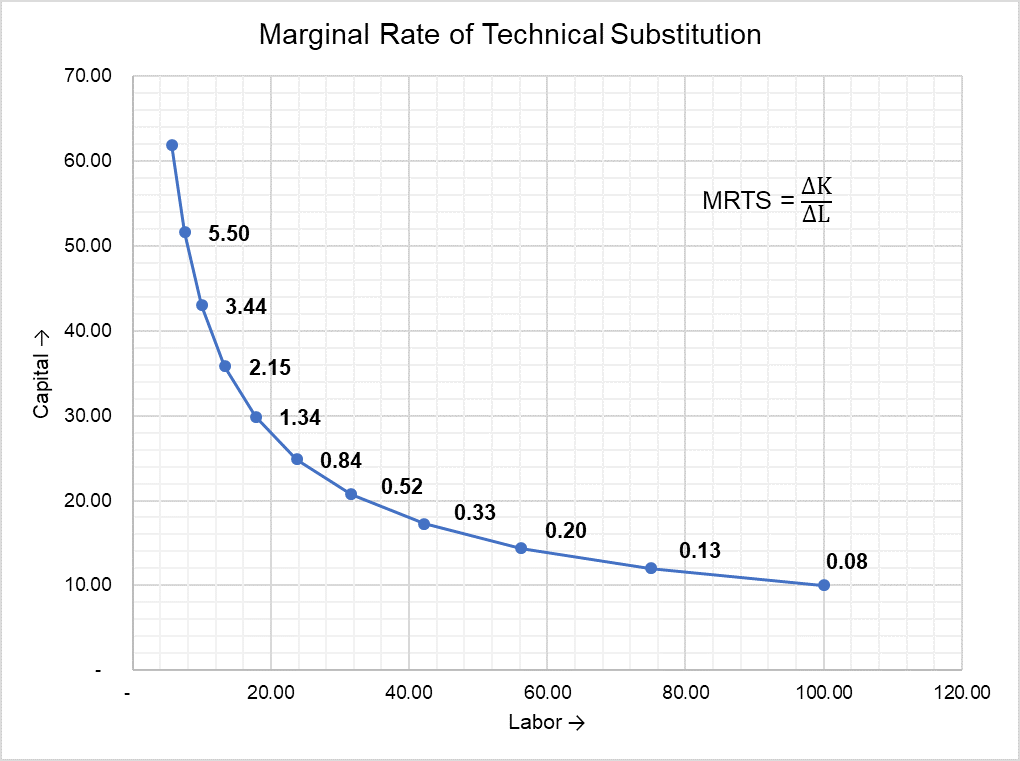
Slope of a curve equals rise (i.e. change in y-axis) over run (i.e. change in x-axis). Marginal rate of technical substitution is equal to ∆K/∆L which is exactly the slope of the above plotted isoquant.
You can see that the rate at which capital is substituted by labor decreases as we move along the isoquant from y-axis to x-axis. It is why the curve gets flatter as it approaches the x-axis. This phenomenon is called diminishing marginal rate of technical substitution.
by Obaidullah Jan, ACA, CFA and last modified on