Marginal Rate of Substitution
Marginal rate of substitution is the rate at which a consumer is willing to replace one good with another. For small changes, the marginal rate of substitution equals the slope of the indifference curve.
An indifference curve is a plot of different bundles of two goods to which a consumer is indifferent i.e. he has no preference for one bundle over the other. If we decrease units of one good, we must compensate the consumer with more units of the other goods in order to maintain the indifference condition. Marginal rate of substitution is the rate at which a decrease in one good must be compensated with an increase in the other good.
Let’s consider a consumer whose indifference bundles for two goods: movies and dine-outs are as follows:
| Bundle | Movies | Dine-outs |
|---|---|---|
| A | 1 | 10.00 |
| B | 2 | 5.00 |
| C | 3 | 3.33 |
| D | 4 | 2.50 |
| E | 5 | 2.00 |
| F | 6 | 1.67 |
If we plot the above bundles, we get the following indifference curve:
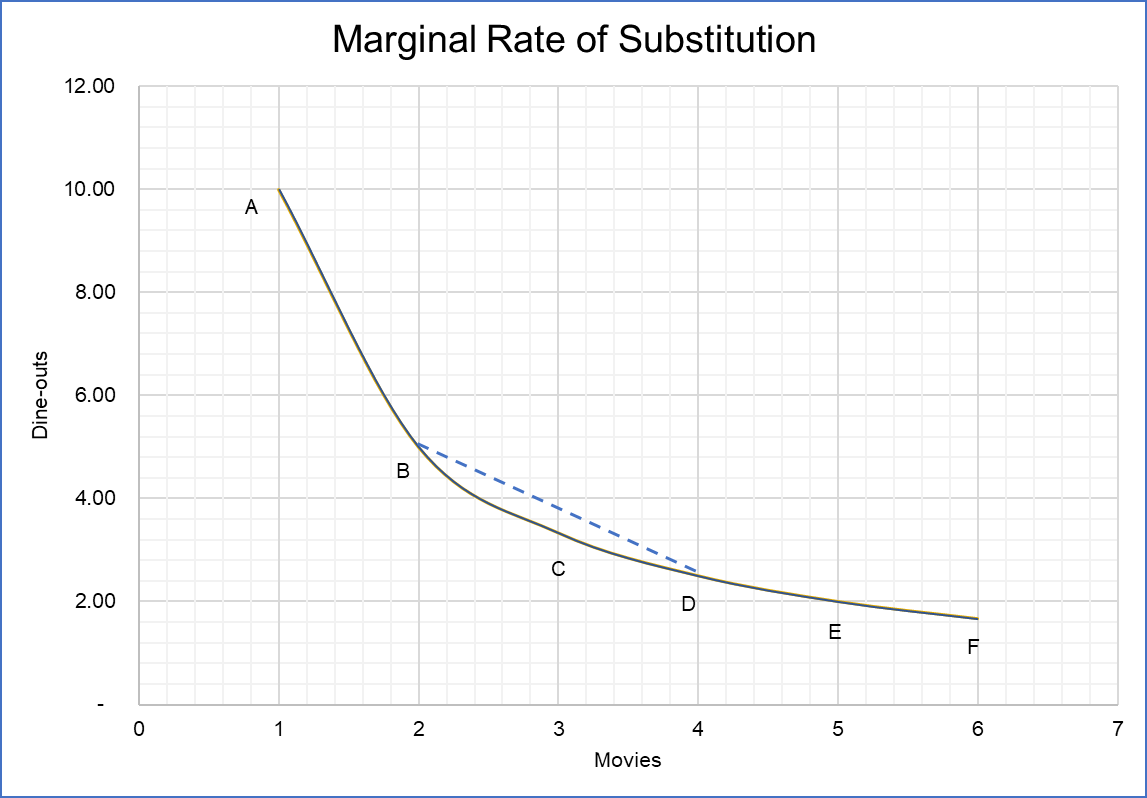
If the consumer moves from Point B to D i.e. he watches 4 movies instead of just 2, he must reduce his dine-outs. The marginal rate of substitution is the rate that dictates how much of dine-outs he must give up to enjoy more movies.
Formula
The law of diminishing marginal utility states that the marginal utility i.e. additional utility of each new unit of a good is lower than the marginal utility of the unit preceding i.e. the first unit of a good has highest utility, the second unit has the second highest utility and so on. Now, if a consumer substitutes one good, say X, with another good, say Y, he must be compensated with the highest units of Y for the first unit of X, second highest units of Y for the second unit of X and so on.
It shows that the marginal rate of substitution continuously changes as we move along an indifference curve. For very small changes in one good, the marginal rate of substitution approaches the slope of the indifference curve which equals change in Y divided by change X. The marginal rate of substitution of X (i.e. movies) with Y (i.e. dine-outs) is defined as follows:
$$ {\rm \text{MRS}} _ {\text{xy}}=-\frac{\text{Y} _ \text{1}-\text{Y} _ \text{0}}{\text{X} _ \text{1}-\text{X} _ \text{0}} $$
MRSxy and MRSyx are not the same, in fact they are reciprocal of each other i.e.
$$ {\text{MRS}} _ {\text{yx}}=\frac{\text{1}}{{\rm \text{MRS}} _ {\text{xy}}} $$
Marginal rate of substitution depends on consumer’s relative preferences i.e. their relative marginal utilities and their starting points. It can be shown that the marginal rate of substitution of y for x equals the price of x divided by y which in turn equals the marginal utility of x divided by marginal utility of y i.e.
$$ {\text{MRS}} _ {\text{xy}}=\frac{\text{P} _ \text{x}}{\text{P} _ \text{y}}=\frac{{\rm \text{MU}} _ \text{x}}{{\rm \text{MU}} _ \text{y}} $$
Indifference curves become flatter as we move from y-axis to x-axis. It is because as y becomes scarce and x become abundant, the marginal rate of substitution for x with y declines. This is called the declining marginal rate of substitution.
by Obaidullah Jan, ACA, CFA and last modified on