Game Theory
In economics, game theory is the study of interaction between different participants in a market. The objective of game theory is to identify the optimal strategy for each participant.
An economic game represents competition between different economic agents. A game typically has three elements: players, strategies and payoffs. A player is a participant in an economic game. Players are typically firms competing with each other, but they could be consumers or a firm and a consumer depending on the context of the game. A strategy is a course of action which either player can adopt. Payoff refers the net benefit or loss that accrue to each player from carrying out his strategy.
A Nash equilibrium is combination of strategies such that no player has any incentive to change its strategy unilaterally.
Types of Economic Games
Games are either simultaneous-move or sequential, static or dynamic, one-off or repeated, cooperative or non-cooperative, etc.
Simultaneous-move Game vs Sequential Game
A simultaneous-move game is a game in which both players must choose their strategies at the same time. No player knows for sure what the other player’s course of action would be.
Examples of simultaneous-move games include:
- Two firms in an oligopoly deciding about their output level (in Cournot model) or price level (in Bertrand model).
- Two prisoners deciding about whether to confess or not in the prisoners’ dilemma.
A sequential game is a game in which one player choses its strategy before the other. The player which decides first typically has a first-mover advantage.
Following are examples of a sequential game:
- Two firms in a Stackelberg model, an oligopoly in which one firm decides about its output level first. The other firm has no option but to cater to the demand which is left-over.
- Two firms are looking to open a retail store in a town which has demand for only one store. The firm which credibly commits to opening the store first wins all the revenue from the new market.
Static Games vs Dynamic Games
A static game is a game which is both simultaneous-move and one-off i.e. there is no repetition and both firms decide at the same time. A dynamic game, on the other hand, is one which is either repeated or sequential.
A repeated game is a game which is played over and over again. Repeated games are further classified into infinitely-repeated games, games which continue forever; and finitely-repeated games, which are exact opposite of infinitely-repeated games.
Cooperative Games vs Non-cooperative Games
A cooperative-game is a game in which both players can communicate and cooperate, and a non-cooperative game is a game in which no cooperation is possible.
Most of the significant economic games are non-cooperative games. For example:
- Firms in an oligopoly can’t collude because it is illegal to fix price or output or even to talk about price, etc. Hence, they engage in non-cooperative games when deciding about their output simultaneously.
- Prisoners in a prisoner’s dilemma can’t communicate. Hence, a prisoners’ dilemma is a non-cooperative game.
Presentation of a Game
A game can be visualized using either a payoff matrix or a decision tree (also called extensive form of a game).
Normal Form
The normal form of a game is a presentation in which the game is visualized using a payoff matrix. A payoff matrix is a table which lists the players of a game, their strategies and their associated payoffs such that the payoff that accrue to the row player is listed first.
Normal form is useful in case of a static game i.e. a game in which both players play the game only once at the same time. Such games are also called one-off simultaneous-move games.
Following is a normal-form presentation of prisoner’s dilemma:
| Payoffs in Prison Terms | Prisoner Q | ||
|---|---|---|---|
| Confess | Do not Confess | ||
| Prisoner P | Confess | -4,-4 | -1,-8 |
| Do not Confess | -8,-1 | -2,-2 | |
Extensive Form
It is better to present a game using a decision tree (also called a game tree) when the game under consideration is a dynamic game i.e. it is repeated or sequential.
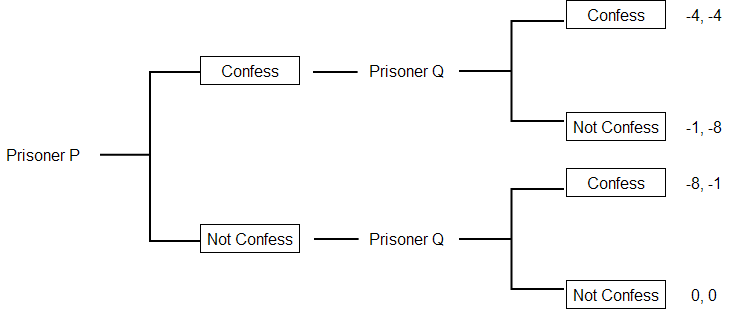
Extensive form of a game is a presentation in which the game is visualized using a decision tree.
The following diagram shows the extensive form of the prisoner’s dilemma.
Types of Strategies
Strategies that players in an economic game can employ are classified into either dominant or dominated, pure or mixed, etc.
Dominant Strategy vs Dominated Strategy
A dominant strategy is a strategy which is optimal regardless of strategy of the other player. A dominant strategy results in the maximum payoff unconditionally i.e. it always results in the best outcome no matter what the opponent does. Not all players/games have dominant strategies.
A dominated strategy is a strategy which generates the worst outcome in all instances. A strategy is dominated if other strategies always generate a better payoff. When one strategy is dominant, other strategies are dominated. A player can have a dominated strategy in a game even if there is no dominant strategy.
Pure Strategy vs Mixed Strategy
A pure strategy is a strategy which has two discrete values i.e. 0 or 1. For example, a firm either advertises or it doesn’t advertise. Similarly, a prisoner either confesses or it doesn’t.
A mixed strategy is a strategy which is a combination of two or more pure strategies based on their expected probabilities.
by Obaidullah Jan, ACA, CFA and last modified on