Minimum Efficient Scale
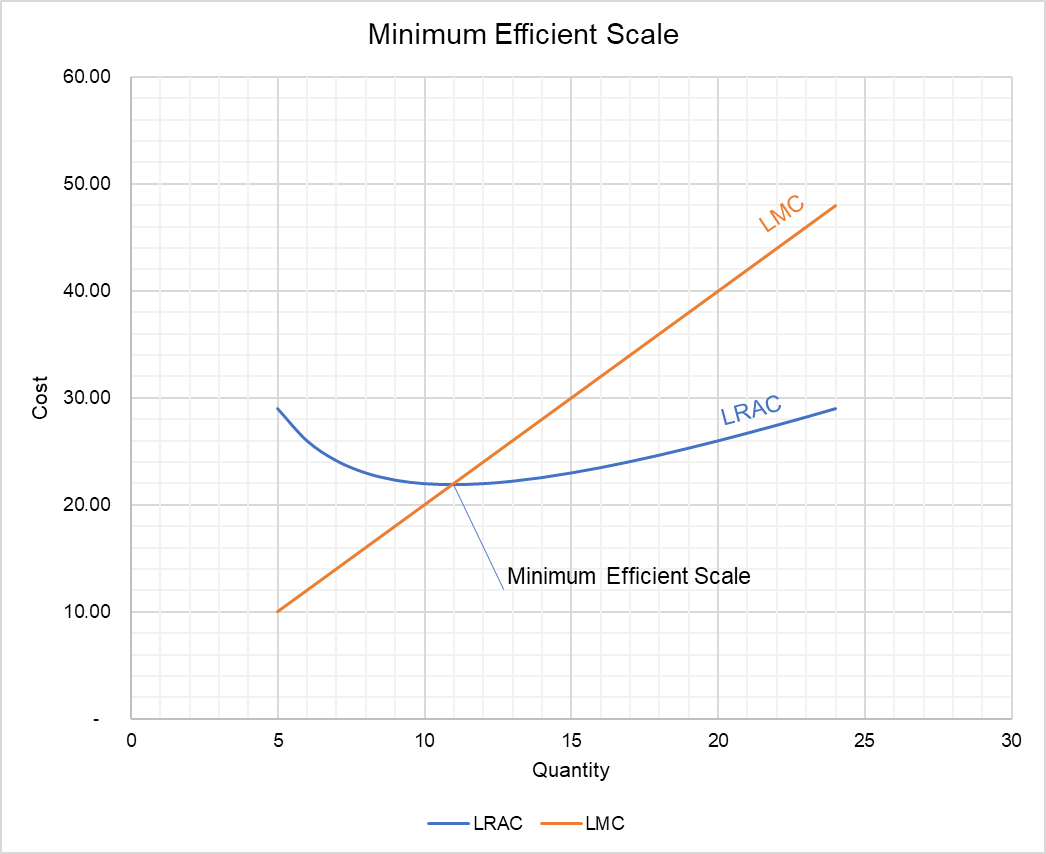
Minimum efficient scale (MES) is the smallest output level at which LRAC is at its minimum. It provides insight about competitiveness of an industry: an industry with high MES typically has few large firms.
Long-run average cost (LRAC) curve is a graph that plots average cost of a firm in the long-run when all inputs can be changed. LRAC is determined by the firm’s expansion path i.e. the combination of labor and capital and other inputs which minimize the firm’s costs at each production level. LRAC initially slopes downward due to economies of scale but as soon as diseconomies of scale set in, it bottoms out and starts to rise. The minimum point of the LRAC represent the firm’s minimum efficient scale.
Minimum efficient scale is an important indicator of an industry’s competitiveness and barriers to entry. If the MES is high, it means that each firm must produce a high proportion of the industry’s output in order to reach the minimum efficient scale. This potentially creates barriers to entry and the industry is expected to be dominated by a few large firms.
Example: Finding MES
One of the property of the long-run cost curves is that the average cost curve is minimum at a point at which the marginal cost curve intersects it from below. It means that the LRAC is minimum at a point at which LRAC and long-run marginal cost (LMC) are equal. This condition can be written as follows:
$$ \text{LMC}\ =\ \text{LRAC} $$
Let’s consider a firm whose long-run total cost curve is given by the following equation:
$$ \text{LRTC}\ =\ \text{120}\ +\ \text{Q}^\text{2} $$
Since the marginal cost equals the slope i.e. the first derivative of the total cost curve, the equation for LMC can be written as follows:
$$ \text{LMC}=\ \text{2Q} $$
Long-run average cost (LRAC) equals LRTC divided by Q:
$$ \text{LRAC}\ =\ \frac{\text{LRTC}}{\text{Q}}\ =\ \frac{\text{120}}{\text{Q}}\ +\ \text{Q} $$
Using the LMC = LRAC relation, we can write the following expression to find the minimum efficient scale:
$$ \text{2Q}\ =\ \frac{\text{120}}{\text{Q}}\ +\ \text{Q} $$
If we solve it, we get Q = 10.95. It shows that the firm’s minimum efficient scale occurs at output close to 12 units.
Graph: LRAC and MES
Let’s verify that the minimum efficient scale occurs at the lowest point on the LRAC by plotting the LRAC and LMC curves.
by Obaidullah Jan, ACA, CFA and last modified on