Marginal Product
Marginal product of a factor of production, for example labor, is the increase in total production that results from one unit increase in the factor of production i.e. labor if other factors, for example capital, are held constant.
Production function shows the relationship between factors of production (also called inputs) such as labor and capital and total production i.e. outputs. As we add more and more of an input, say labor, generally the total units produced increase and vice versa. The marginal product of an input refers to the increase in total production that results from the last unit of the input.
It is important to keep all factors other than the factor for which marginal product is being calculated constant otherwise the increase in total production will represent the combined effect of changes in all factors. For example, in finding out marginal product of labor, we need to keep land, capital, technology, etc. constant to filter out the change in output that results from change in labor.
Mathematically, marginal product equals total production at n units of input minus total production at n -1 units of input. Marginal product function can be written as follows:
$$ \text{MP}=\frac{\text{Q} _ \text{n}\ -\ \text{Q} _ {\text{n}-\text{1}}}{\text{L} _ \text{n}-\text{L} _ {\text{n}-\text{1}}} $$
Where Qn and Qn-1 represent the total production at n and n – 1 units of the inputs respectively. Similarly, Ln and Ln-1 stand for n and n – 1units of input.
Example
Skyler White is the owner of A1A car wash. She wants to find out what happens to her sales if she hires more people. The following table shows how the total production (in number of washes) changes if labor changes:
| Staff | Total Washes (Total Product) | Marginal Washes (Marginal Product) |
|---|---|---|
| 0 | 0 | |
| 1 | 10 | 10 |
| 2 | 19 | 9 |
| 3 | 27 | 8 |
| 4 | 34 | 7 |
| 5 | 40 | 6 |
| 6 | 45 | 5 |
| 7 | 49 | 4 |
The marginal product of the first unit is 10 because the first employee can wash 10 cars in a day. The marginal product of the second employ is 9 (=19 – 10). It is lower than the marginal product of the first employee presumably because they waste some time in gossiping about Whites. The marginal product of third employee is 8 (=27 – 19) and so on. In finding out the marginal product, we have assumed there are no other changes i.e. there is no investment in new tools, etc.
Skyler should make sure that the revenue of the marginal product of the last employee is higher or equal to the wages she pays to the last employee.
The following chart plots total product and marginal product of A1A car wash.
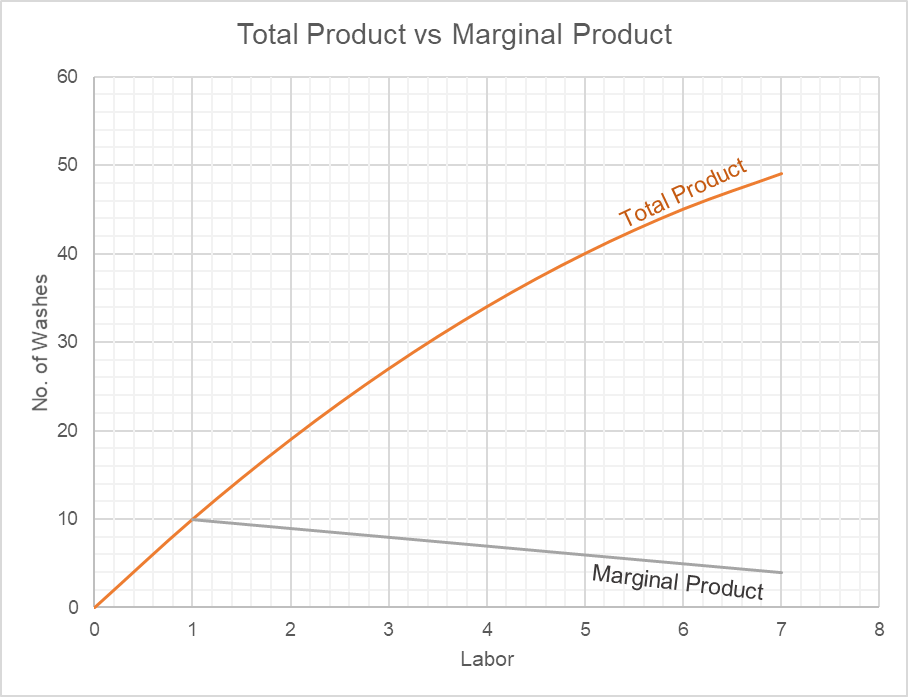
Pleas note that the total product curves slope upwards but at a flatter rate while the marginal product curves downward.
Another measure of production is the average production which equals total production divided by total units of the input. For example, the average product of the seventh employee is 7 (i.e. 49 divided by 7).
by Obaidullah Jan, ACA, CFA and last modified on