Marginal Product of Capital
Marginal product of capital (MPK) is the incremental increase in total production that results from one unit increase in capital while keeping all other inputs constant.
Identifying the marginal product of capital is important because firms take investment decisions by comparing their marginal product of capital with their cost of capital. When the marginal product of capital is higher than the cost of capital, it makes sense to increase production by increasing capital but as soon as marginal product of capital falls below the cost of capital, adding any more capital results in a decrease in the firm’s profit.
An economy’s total production is best represented in most cases by the Cobb-Douglas production function with constant returns to scale. Under the Cobb-Douglas model, an economy’s total production (Y) depends on its total factor productivity (A), its stock of labor (L) and capital (K) and the responsiveness of Y to each input:
$$ \text{Y}=\text{A}\times \text{K}^\alpha\times \text{L}^{\text{1}-\alpha} $$
α represents the proportion of capital and 1- α represents the proportion of labor required for production to occur.
When an economy has constant returns to scale, any increase in capital while keeping labor constant results in diminishing marginal product of capital as illustrated in the example below.
Calculation
Marginal product of capital of an economy which is represented by the Cobb-Douglas production function can be calculated using the following formula:
$$ \text{MPK}=\alpha\times \text{A}\times \text{K}^{\alpha-\text{1}}\times \text{L}^{\text{1}-\alpha}=\alpha\times\frac{\text{Y}}{\text{K}} $$
The equations above are derived using a bit of calculus i.e. by differentiating the Cobb-Douglas function with respect to K by keeping L constant.
$$ \text{MPK}=\frac{\partial \text{Y}}{\partial \text{K}}=\frac{\partial \text{A} \text{K}^\alpha \text{L}^{\text{1}-\alpha}}{\partial \text{K}} $$
$$ \text{MPK}=\alpha\times \text{AK}^{\alpha-\text{1}}\text{L}^{\text{1}-\alpha} $$
Moving Kα-1 to the denominator gives us the following expression:
$$ \text{MPK}=\alpha\times \text{A}\times\frac{\text{L}^{\text{1}-\alpha}}{\text{K}^{\text{1}-\alpha}} $$
Multiplying and dividing the right-hand side of the above equation with Kα, we get:
$$ \text{MPK}=\alpha\times \text{A}\times\frac{\text{L}^{\text{1}-\alpha}}{\text{K}^{\text{1}-\alpha}}\times\frac{\text{K}^\alpha}{\text{K}^\alpha} $$
A bit of rearrangement:
$$ \text{MPK}=\alpha\times\frac{\text{A}\times \text{K}^\alpha\times \text{L}^{\text{1}-\alpha}}{\text{K}^{\text{1}-\alpha+-\alpha}} $$
The numerator exactly equals Y and the denominator reduces to K:
$$ \text{MPK}=\alpha\times\frac{\text{Y}}{\text{K}} $$
Example and Graph
Let’s consider an economy which produces only baby strollers and whose production is represented by the following equation:
$$ \text{Y}=\text{2,000}\times \text{K}^{\text{0.5}}\times \text{L}^{\text{0.5}} $$
The following table shows the total number of baby strollers produced when the number of manufacturing plants increase but the trained labor available to operate them remains constant.
| Number of Plants | Number of Workers | Total Production | Marginal Product |
|---|---|---|---|
| 0 | 500 | - | - |
| 1 | 500 | 44,721 | 44,721 |
| 2 | 500 | 63,246 | 18,524 |
| 3 | 500 | 77,460 | 14,214 |
| 4 | 500 | 89,443 | 11,983 |
| 5 | 500 | 100,000 | 10,557 |
| 6 | 500 | 109,545 | 9,545 |
| 7 | 500 | 118,322 | 8,777 |
The following chart shows total production on y-axis and capital, K on x-axis.
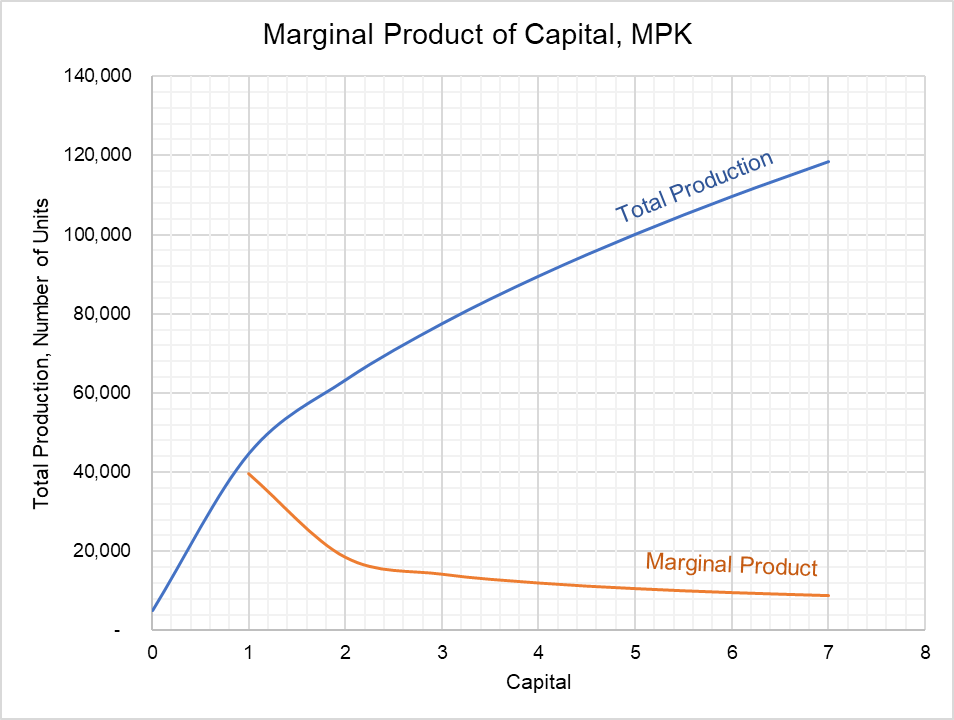
The total production curve gets flatter as more and more capital is added while keeping labor constant. It is because when capital increases without associated increase in labor, there are not enough people to operate the machines and hence the increase in production is lower.
by Obaidullah Jan, ACA, CFA and last modified on