Future Value Factor
Future value factor (FVF) (also called the future value interest factor (FVIF)) is the equivalent value at some future date of a cash flow at time 0 or a series of cash flows that occur after equal time interval. It is used to calculate the future value of a single sum or future value of an annuity or annuity due by multiplying the cash flow with the relevant future value factor.
A future value factor table lists the future value factors for different periodic interest rates and number of periods. Such a table is useful in manual calculation of future values of a single sum or an annuity. All you need to do it to find out the factor at the intersection of the periodic interest and relevant time period and multiply it with the cash flow.
Example
Let’s say you want to find out future value of $10,000 after 3 years when the annual percentage rate is 12% and there are two compounding periods per year. The periodic interest rate is 6% (i.e. APR of 12% divided by 2) and the number of periods is 6 (i.e. 3 years multiplied by 2). From the following table, we see that the future value factor at the intersection of 5% periodic interest rate and 6 number of periods is 1.4185.
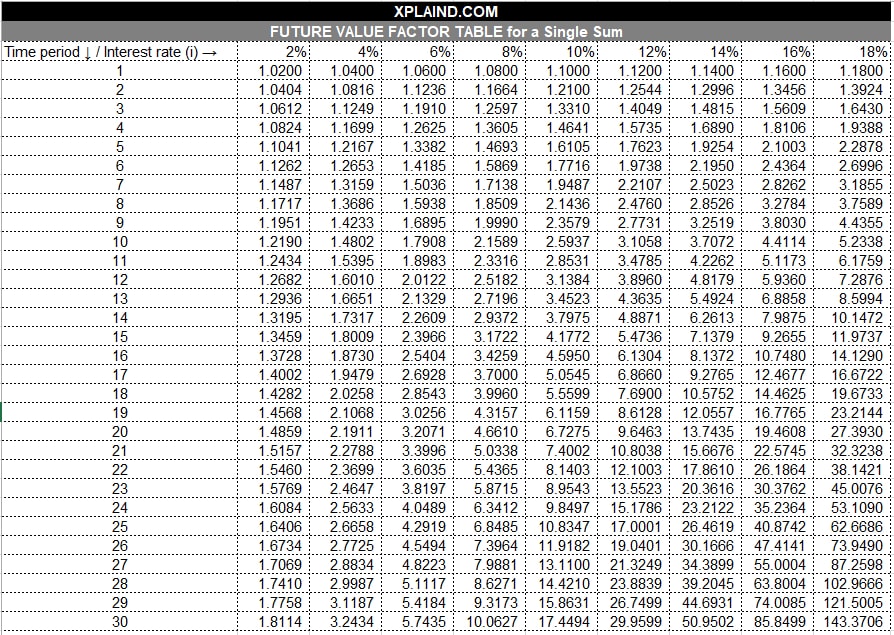
The future value equals $14,185 (i.e. $10,000 multiplied by 1.4185).
Formula
We can get the same results using the formula approach. Following is the formula to calculate the future value factor of a single sum:
FVF = (1 + APR/m)(n×m)
Where APR is the annual nominal percentage rate, m is the number of compounding periods per year and n is the total number of years.
Given the data in the above example, FVF is 1.4185
FVF = (1 + 12%/2)(3×2) = 1.4185
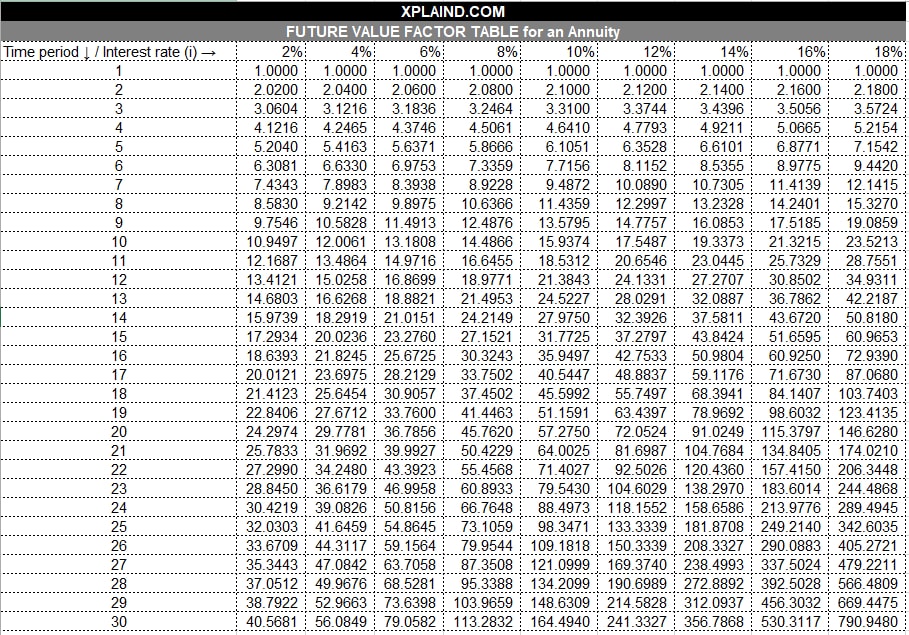
Following are the formulas for future value factor of an ordinary annuity:
| FVF of Ordinary Annuity = | (1 + APR/m)(n×m) − 1 |
| APR/m |
Future value factor of an annuity due can be determined by multiplying the FVF of an (ordinary) annuity with (1 + APR/m):
FVF of Annuity Due = FVF of Ordinary Annuity × (1 + APR/m)
Alternatively, you can use the following future value factor table to calculate future value of an annuity:
by Obaidullah Jan, ACA, CFA and last modified on