Negative Amortization
Negative amortization is where the principal balance on a loan increases initially because the periodic payments being made are not enough to pay off the interest accrued on the loan. The unpaid interest is added to the principal balance of the loan and periodic payments are recalculated at some future date.
An amortizing loan is a loan whose periodic payments have both interest and principal repayment components. As the loan nears its maturity, the loan’s principal balance and the interest accrued in each subsequent period decreases and the principal repayment component included in each periodic payment increases. A negative amortization loan is exactly opposite to an amortizing loan for at least some portion of the loan term. A loan can’t remain in negative amortization mode forever because the principal balance must be paid off. Negative amortization loans either have a fixed date at which the negative amortization stops and the loan repayment amount is calculated based on the remaining amortization period or they have a maximum limit on principal which once reached triggers amortization over the remaining life of the loan.
Example
You study for a business degree at university which has very generous financial assistance program. You obtained a $100,000 at 5% per annum on 1 January 2015. Your program ends on 31 December 2017. You are required to a payment of $300 only in the initial 3 years. Afterwards, you will be required to make the actual required monthly payment to repay the loan by 31 December 2030. Let’s see how negative amortization works.
No interest amount is accrued during your program so the principal balance of the loan as at 31 December 2017 is $100,000.
The monthly interest expense for January 2018 would be $417 (=$100,000 × 5% × 1/12). Because you are paying only $300 each month, the difference of $117 (=$417 - $300) must be added to the principal balance. Interest expense in February 2018 would be $417.15 (=($100,00 + $117) × 5% × 1/12) and the amount added to principal balance would be $117.15. This will continue till the end of the initial 3 years grace period when the principal balance would be $104,521.
Your monthly payment requirement will be recalculated at the end of grace period. The remaining term of the loan is 10 years (i.e. 120 months), the monthly interest rate is 0.417% and the monthly payment requirement is $1,109. This figure is determined using the formula for present value of an annuity:
$$ \text{PMT}=\frac{\text{\$104,521}}{\frac{\text{1}-{(\text{1}+\text{0.417%})}^{-\text{120}}}{\text{0.417%}}}=\text{\$1,109} $$
The following chart shows the behavior of principal balance, interest expense and periodic payment when there is negative amortization:
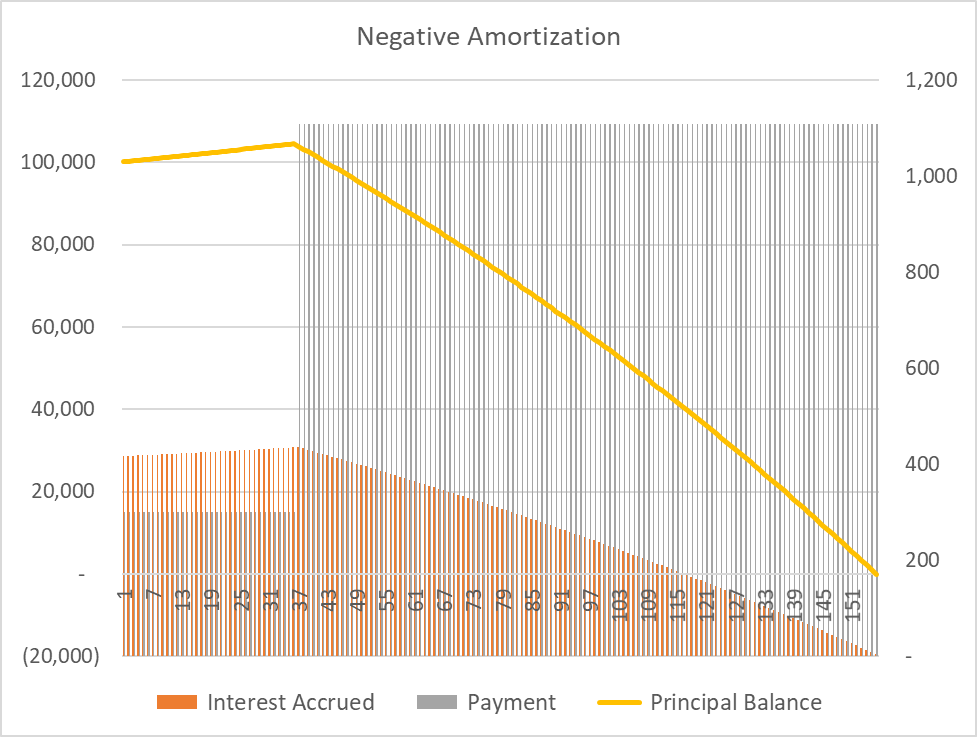
Negative amortization is in place during the time when
by Obaidullah Jan, ACA, CFA and last modified on