Bond Yield
A bond’s yield is the expected rate of return on a bond. The are three measures of bond yield: nominal yield, current yield and yield to maturity.
In bond markets, a bond price movements are typically communicated by quoting their yields. It is because it is a standardized measure which makes comparison between different bonds easier. Unlike the bond price which depends on the denomination i.e. par value of the bond, yield doesn’t depend on whether the par value is $100 or $1,000. It also helps us determine the spread i.e. the yield difference between different types of bonds and associate the spreads to different risks.
Relationship between Bond Yield and Bond Price
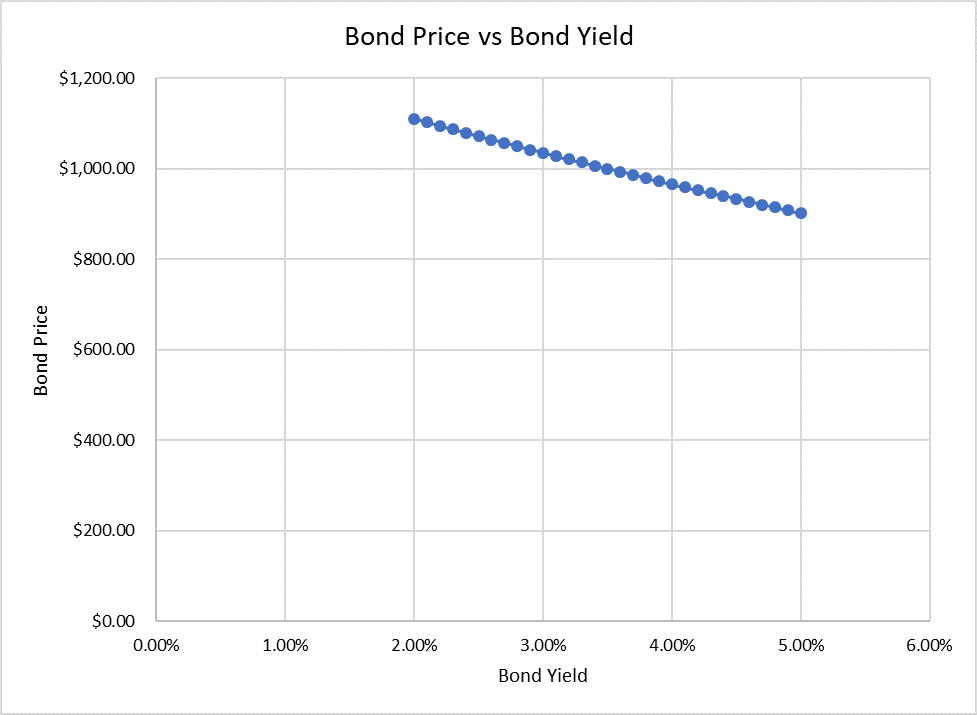
There is an interesting relationship between bond price and bond yield. As a bond’s price drops, its yield rises and vice versa.
If a bond’s coupon rate is lower than the bond’s yield, it means that the bond is trading at a discount to its par value i.e. it current market price is lower than its maturity value. If someone purchases the bond at that lower market price and holds it till maturity, his ultimate return will be higher than the coupon rate because it will comprise of the interest payments and the capital gain that results from the difference between the purchase price of the bond and the face value. The opposite is true if the bond’s yield is lower than its coupon rate i.e. the bond sells at a premium.
Nominal Yield (i.e. Coupon Rate)
Nominal yield equals a bond's annual coupon rate. The coupon rate is the annual percentage rate which is applied to the face value of the bond to work out the periodic coupon payment.
While the coupon rate is important in determining the periodic cash flow of the bond, it is not a very comprehensive measure of the bond’s ultimate return. It is because it doesn’t take in to consideration the difference between the current market price and the face value of the bond. For example, a bond might pay a very high coupon rate, but its current price might be lower than its face value due to high market interest rate. The nominal yield measure doesn’t capture this price movement.
It also doesn’t include the effect of any initial discount or premium on the bond. Further, since zero-coupon bonds have no coupon payments, there is no coupon rate to use as a yield measure.
Current Yield
The current yield is a better measure than the nominal yield because it measures the return with reference to the current market price of the bond. However, it is still doesn’t accommodate the effect of price movement between the date the bond was purchased and the date of valuation. Current yield is calculated using the following formula:
| Current Yield = | F × c |
| P0 |
Where c is the annual coupon rate, F is the face value of the bond and P is its current market price. Current yield of a bond that trades below its face value is higher than its nominal yield (i.e. coupon rate) and vice versa.
Yield to Maturity (Redemption Yield)
The most useful and theoretically-sound measure of bond yield is the yield to maturity of the bond. There are other measures such as current yield, but they are less comprehensive.
The yield to maturity is the rate of return that a bondholder expects to earn if he purchases the bond at its current price (P0) and holds its till maturity and receives all associated future coupon payments and the maturity value. It is effectively the internal rate of return of the bond. It is the periodic rate which causes the discounted value of bond cash flows (coupon payments and face value) to equal the bond’s current market price.
Formula
Yield to maturity can be calculated by solving the following equation for YTM:
| P0 = | c | × | (1 + YTM/m)−(n×m) | + | F |
| m | YTM/m | (1+YTM/m)(n×m) |
Where P0 is the current bond price, c is the annual coupon rate, m is the number of coupon payments per year, YTM is the yield to maturity, n is the number of years the bond has till maturity and F is the face value of the bond.
The above equation must be solved through hit-and-trial method, i.e. you plug-in different numbers till you get the right hand side of the equation equal to the left-hand side. An easier alternative is the use to Microsoft Excel RATE function.
Yield to maturity has the same weakness as that of the internal rate of return. It assumes that the coupon payments are reinvested at the yield to maturity. It understates the reinvestment risk.
Example
Let’s say we have a $1,000-par value bond issued on 1 January 2011 paying 3.5% semi-annual coupons. The bond had a maturity of 10 years when issued. Calculate the bond’s yield to maturity at the following dates and prices:
| Date | 1-Jan-13 | 1-Jan-15 | 1-Jan-16 | 1-Jan-18 |
|---|---|---|---|---|
| Price | $1,015 | $990 | $950 | $1,030 |
As at 1 Jan 2013, the bond has 8 years till maturity, its coupon rate is 3.5% which is paid twice a year, the current price is $1,015 so we can create the following equation to solve for yield to maturity:
| $1,015 = | 3.5% | × | (1 + YTM/2)−(8 × 2) | + | $1,000 |
| 2 | YTM/2 | (1+YTM/2)(8 × 2) |
Because the bond is trading at price above its face value, so the yield must be lower than the coupon rate. If we enter 3.25% as yield to maturity, the right-hand side of the above equation works out to $1,017.49:
| Pi = | 3.5% | × | (1 + 3.25%/2)−(8×2) | + | $1,000 | = $1,017.49 |
| 2 | 3.25%/2 | (1+3.25%/2)(8×2) |
The right-side of the equation sums to value higher than the current price, so we know we must try a yield to maturity that’s slightly higher than the value we previously entered. If we enter 3.3%, the right-hand side of the equation amounts to $1,013.96 .
| Pii = | 3.3% | × | (1 + 3.3%/2)−(8×2) | + | $1,000 | = $1,013.96 |
| 2 | 3.3%/2 | (1+3.3%/2)(8×2) |
The bond price we arrive at by entering 3.3% is now lower than the current market price. We must slightly reduce our yield to maturity estimate. Using this trial-and-error process, the right-hand side of the above equation equals $1,015, the current market price of the bond at 3.285%. This is the yield to maturity of the bond.
Instead of the hit and trial method, we can use Microsoft Excel RATE function. The RATE function syntax is RATE(nper, pmt, pv, [fv], [type], [guess]). In the above scenario, our formula will look like as follows: RATE(8*2,-3.5%/2*1000,1015,-1000). The yield to maturity obtained using the RATE function is the semi-annual rate, which can be converted to the annual rate by multiplying it with 2.
Similarly, we can work out yield to maturity on the remaining dates. The following table summarizes the yield corresponding to the given prices and years till maturity:
| Date | 1-Jan-13 | 1-Jan-15 | 1-Jan-16 | 1-Jan-18 |
|---|---|---|---|---|
| Price | $1,015 | $990 | $950 | $1,030 |
| Yield to maturity | 3.29% | 3.69% | 4.63% | 2.46% |
You can see that the price and the yield move in opposite directions.
by Obaidullah Jan, ACA, CFA and last modified on