Yield to Maturity (YTM)
Yield to maturity (YTM) is the annual return that a bond is expected to generate if it is held till its maturity given its coupon rate, payment frequency and current market price.
Yield to maturity is essentially the internal rate of return of a bond i.e. the discount rate at which the present value of a bond’s coupon payments and maturity value is equal to its current market price.
Even though it is not a perfect measure of cost of debt, it is better than the current yield and/or coupon rate. It is why it is an important input in determining a company’s weighted average cost of capital.
Yield to maturity of a bond can be worked out by iteration, linear-interpolation, approximation formula or using spreadsheet functions.
Iteration method
The iteration method of calculating yield to maturity involves plugging in different discount rate values in the bond price function till the present value of bond cash flows (right-hand side of the following equation) matches the bond price (left-hand side):
| P = c × F × | 1 − (1 + r)-t | + | F |
| r | (1 + r)t |
Where P is the bond price i.e. the price at which the bond is currently trading, F is the face value of the both (which is also its maturity value i.e. the value which the bond issuer will return to the bondholder at maturity), c is the periodic coupon rate, t is the number of coupon payments till maturity of the bond and r is the periodic yield to maturity.
Annual yield to maturity equals periodic yield to maturity multiplied by number of coupon payments per year:
Annual Yield to Maturity = Periodic Yield to Maturity × No of Coupon Payments
If we know P, c, F, m and n, we can solve for r by trying different values.
Linear-interpolation method
There is an inverse relationship between bond price and bond yield which means that if price is low, yield must be high and vice versa. We can use this relationship to find yield to maturity using the linear interpolation as follows:
- STEP 1: Check if the bond price is lower than the face value. If yes, yield to maturity must be higher than the coupon rate. If no, yield to maturity is lower than the coupon rate.
- STEP 2: Keeping the result from Step 1 in view, set a low r value rL such that the present value of bond cash flows PVL is higher than the bond price.
- STEP 3: Set a high r value rH such that the present value of bond cash flows PVH is lower than the bond-price.
- STEP 4: Use the following equation to solve for yield to maturity r:
| r = rL + | PVL | × (rH − rL) |
| PVL − PVH |
Approximation formula
Yield to maturity can also be calculated using the following approximation formula:
| YTM = | C + (F − P)/n |
| (F + P)/2 |
Where C is the annual coupon amount, F is the face value of the bond, P is the current bond price and n is the total number of years till maturity.
Alternatively, we can also use Microsoft Excel YLD function to find yield to maturity.
Illustrative example
Company D's 10-year bond with par value of $1,000 and semiannual coupon of 8% is currently trading at $950.
Find the yield to maturity on the bond.
Company D's bond has a par value of $1,000; semiannual coupon of $40 (=8%/2×$1,000); current market price of $950, and payment frequency of 2 per year.
We can set-up the bond-price equation with the given data as follows:
| $950 = 8%/2 × $1,000 × | 1 − (1 + r)-2×10 | + | $1,000 |
| r | (1 + r)2×10 |
Interpolation Method
Let us try the iteration method first:
We know that:
- If yield to maturity is equal to the coupon rate, the bond is trading at par;
- If the yield to maturity is lower than the coupon rate, the bond will be trading above par (which means it is trading at premium); and
- If the yield to maturity is higher than the coupon rate, the bond will be trading below par (which means it trading at discount).
In the example above, price (of $950) is lower than the par value of $1,000. This tells us that the yield to maturity must be higher than the coupon rate of 8%. We select an annual discount rate above 8%, say 8.5% (which corresponds to periodic discount rate of 4.25%). At this rate, the present value of bond cash-flows (right-hand side) works out to $966.76.
Similarly, at annual discount rate of 9%, PV of bond cash flows is $934.96. From this we follow that we need to focus on discount rates between 8.5% and 9%. The iteration method requires us to keep trying different values till we narrow down on a rate which equates the present value of bond cash flows (right-hand side) to bond price (left-hand side).
Linear-Interpolation Method
From the iteration calculations so far, we know that at the lower discount rate rL of 8.5%, PVL is $966.76 and at the higher discount rate rH of 9%, PVH is $934.96. Plugging these numbers into the linear-interpolation formula gives us an estimated yield to maturity of 8.75%.
| r = 8% + | $966.76 | × (9% − 8%) = 8.75% |
| $966.76 − $934.96 |
Approximation Formula
We know that annual coupon C is $80, face value F is $1,000, price P is $950 and n is 10. Plugging these numbers, we find that approximate yield to maturity is 8.72%.
| YTM = | $80 + ($1,000 − $950)/10 | = 8.72% |
| ($1,000 + $950)/2 |
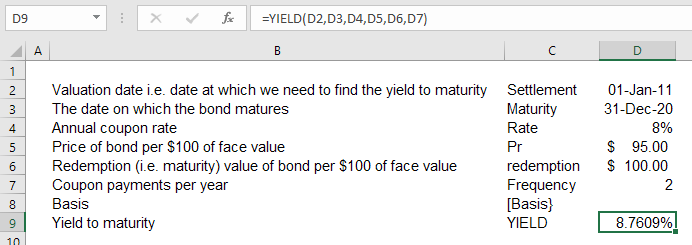
Yield to Maturity using YIELD Function
The method that gives us the most accurate measure of yield to maturity is Microsoft Excel YIELD function. We need to assume the bond issue date and maturity date such that the time to maturity is 10 years.
Limitation of yield to maturity
Yield to maturity carries the same drawback as the internal rate of return: it assumes that the bond’s coupon payments are reinvested at the yield to maturity which is not normally the case. If coupons are to be reinvested at lower rates, yield to maturity will be an overstated measure of return on bond (and cost of debt). In other words, yield to maturity does not address a bond’s reinvestment risk.
Further, yield to maturity is valid only when bond is held till maturity. If the bond is disposed off earlier, it is quite possible that it may fetch a price lower than the face value.
There are many other similar measures used such as yield to call, yield to put, cash flows yield, etc.
by Obaidullah Jan, ACA, CFA and last modified on