Spot Interest Rate
Spot interest rate for maturity of X years refers to the yield to maturity on a zero-coupon bond with X years till maturity. They are used to (a) determine the no-arbitrage value of a bond, (b) determine the implied forward interest rates through the process called bootstrapping and (c) plot the yield curve.
A zero-coupon bond is a debt instrument that pays its face value i.e. principal back at its maturity date. It does not make any other payments to the bond-holder. The yield on such an instrument is a direct measure of required return for the given maturity. The price of a zero-coupon bond equals the present value of its face value. This relationship can be expressed as follows:
$$ \text{P}=\frac{\text{FV}}{\left(\text{1}+\frac{\text{YTM}}{\text{m}}\right)^{\text{n}\times \text{m}}} $$
Where FV is the face value of the bond, YTM is the yield to maturity, m is the number of compounding periods per year and n is the number of years till maturity. By rearranging the above expression, we can work out the formula for yield to maturity on a zero-coupon bond:
$$ \text{s} _ \text{n}=\text{YTM}=\left[\left(\frac{\text{FV}}{\text{P}}\right)^\frac{\text{1}}{\text{n}\times \text{m}}-\text{1}\right]\times \text{m} $$
The yield to maturity calculated above is the spot interest rate (sn) for n years.
By determining spot interest rates corresponding to each cash flow of a bond and then discounting each cash flow using that period-specific yield, we can determine the no-arbitrage price of a bond.
Example: Spot Interest Rates and Yield curve
Let’s see how we can create the yield curve from the following current market prices of zero-coupon bonds with bi-annual compounding:
| Current Price | Maturity (in Years) |
|---|---|
| 98.50 | 1 |
| 94.10 | 3 |
| 84.00 | 5 |
| 58.20 | 10 |
| 38.50 | 15 |
| 16.25 | 25 |
The following table shows relevant spot-rates:
| Current Price | Maturity (in Years) | Spot Interest Rates |
|---|---|---|
| 98.50 | 1 | 1.52% |
| 94.10 | 3 | 2.04% |
| 84.00 | 5 | 3.52% |
| 58.20 | 10 | 5.49% |
| 38.50 | 15 | 6.47% |
| 16.25 | 25 | 7.40% |
We illustrate how to determine the spot rate for the bond with 15 years till maturity as follows:
$$ \text{s} _ {\text{15}}=\left[\left(\frac{\text{\$100}}{\text{\$38.50}}\right)^\frac{\text{1}}{\text{15}\times\text{2}}-\text{1}\right]\times\text{2}=\text{6.47%} $$
If we plot the above schedule of spot interest rates with reference to their maturities, we get the yield curve:
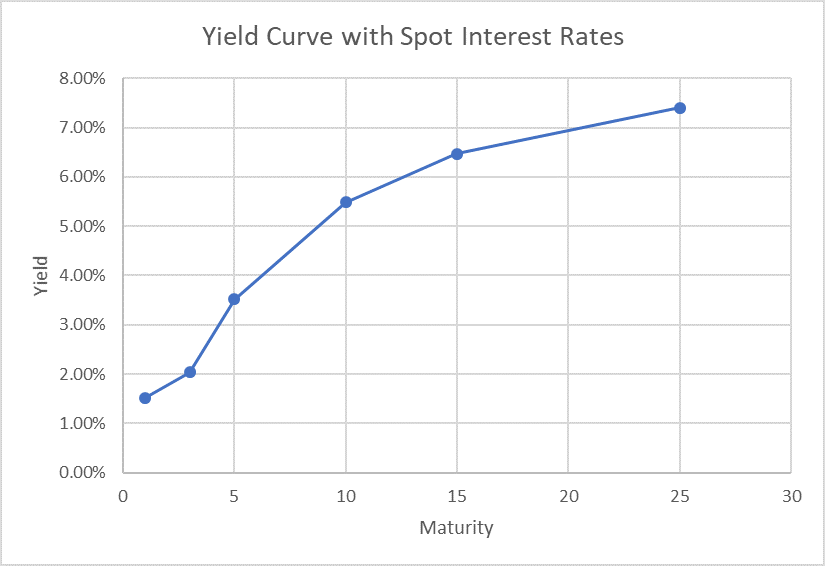
Spot Interest Rate vs Yield to Maturity
Yield to maturity and spot interest rate in case of pure-discount bonds i.e. zero-coupon bonds are the same. However, in case of coupon-paying bonds, yield to maturity is the (somewhat) weighted average of the individual spot interest rates that apply to each cash flow of the bond.
Let’s say we have a 3- year bond with face value of $100 and annual coupon of $2.00. The spot interest rates for 1, 2 and 3 years are 1.50%, 1.75% and 1.95%.
The following equation describes the relationship between yield to maturity of the bond and the relevant spot interest rates:
$$ \frac{\text{\$2}}{({\text{1}+\text{YTM})}^\text{1}}+\frac{\text{\$2}}{({\text{1}+\text{YTM})}^\text{2}}+\frac{\text{\$100}+\text{\$2}}{({\text{1}+\text{YTM})}^\text{2}}\\=\frac{\text{\$2}}{({\text{1}+\text{1.50%})}^\text{1}}+\frac{\text{\$2}}{({\text{1}+\text{1.75%})}^\text{2}}+\frac{\text{\$100}+\text{\$2}}{({\text{1}+\text{1.95%})}^\text{3}} $$
What we have done is to find the no-arbitrage price of the bond using the spot interest rates (on the right-hand side of the equation). The left-hand side calculates the yield to maturity (i.e. internal rate of return) of the bond as the rate that equates its future cash flows to its no-arbitrage price.
The no-arbitrage price (i.e. right-hand side) works out to $102.33 which yields 1.94% (i.e. the left hand side).
by Obaidullah Jan, ACA, CFA and last modified on