Bond Convexity
Convexity of a bond is the phenomena that causes the increase in bond price due to a decrease in interest rates to be higher than the decrease in bond price owing to an increase in interest rates. It represents the change in duration that occurs due to change in bond yield. High convexity means higher sensitivity of bond price to interest rate changes.
A bond’ intrinsic value equals the present value of its future cash flows i.e. coupon payments and maturity value. The following equation mathematically expresses the relationship:
$$ \text{P}=\frac{\text{c}}{\text{m}}\times \text{F}\times\frac{\text{1}-{(\text{1}+\frac{\text{r}}{\text{m}})}^{-\text{n}\times \text{m}}}{\frac{\text{r}}{\text{m}}}+\frac{\text{F}}{{(\text{1}+\frac{\text{r}}{\text{m}})}^{\text{n}\times \text{m}}} $$
Where P is the current price of the bond, c is the annual coupon rate, F is the face value of the bond, r is the annual yield on the bond, m is the number of coupon payments per year and n is the total years to maturity.
It follows from the above equation that the bond price P falls with increase in the market interest rate r and vice versa.
Let’s say you have a 10-year $1,000 face value bond paying 5% coupon rate twice a year. If the market interest rate is equal to the coupon rate i.e. 5%, the bond price exactly equals the face value as illustrated below:
$$ \text{P} _ \text{0}=\frac{\text{5%}}{\text{2}}\times\text{\$1,000}\times\frac{\text{1}-{(\text{1}+\frac{\text{5%}}{\text{2}})}^{-\text{10}\times\text{2}}}{\frac{\text{5%}}{\text{2}}}+\frac{\text{\$1,000}}{{(\text{1}+\frac{\text{5%}}{\text{2}})}^{\text{10}\times\text{2}}}=\text{\$1,000} $$
If the market interest rates fall to 4.8%, the new bond price will be $1,015.74 representing a 1.57% change as shown below:
$$ \text{P} _ \text{d}=\frac{\text{4.8%}}{\text{2}}\times\text{\$1,000}\times\frac{\text{1}-{(\text{1}+\frac{\text{4.8%}}{\text{2}})}^{-\text{10}\times\text{2}}}{\frac{\text{4.8%}}{\text{2}}}+\frac{\text{\$1,000}}{{(\text{1}+\frac{\text{4.8%}}{\text{2}})}^{\text{10}\times\text{2}}}=\text{\$1,015.74} $$
However, if the interest rates increase by the same magnitude i.e. 0.2% to 5.2%, the bond price drops to $984.56 representing a decline of 1.54% from face value:
$$ \text{P} _ \text{i}=\frac{\text{5.2%}}{\text{2}}\times\text{\$1,000}\times\frac{\text{1}-{(\text{1}+\frac{\text{5.2%}}{\text{2}})}^{-\text{10}\times\text{2}}}{\frac{\text{5.2%}}{\text{2}}}+\frac{\text{\$1,000}}{{(\text{1}+\frac{\text{5.2%}}{\text{2}})}^{\text{10}\times\text{2}}}=\text{\$984.56} $$
The following table shows the bond price at different market interest rates:
| Market Interest Rate | Bond Price |
|---|---|
| 0% | $1,500 |
| 1% | $1,380 |
| 2% | $1,271 |
| 3% | $1,172 |
| 4% | $1,082 |
| 5% | $1,000 |
| 6% | $926 |
| 7% | $858 |
| 8% | $796 |
| 9% | $740 |
| 10% | $688 |
| 11% | $641 |
| 12% | $599 |
| 13% | $559 |
| 14% | $523 |
| 15% | $490 |
| 16% | $460 |
| 17% | $432 |
| 18% | $407 |
| 19% | $383 |
| 20% | $361 |
If we plot the bond price against the market interest rates, we get the following graph:
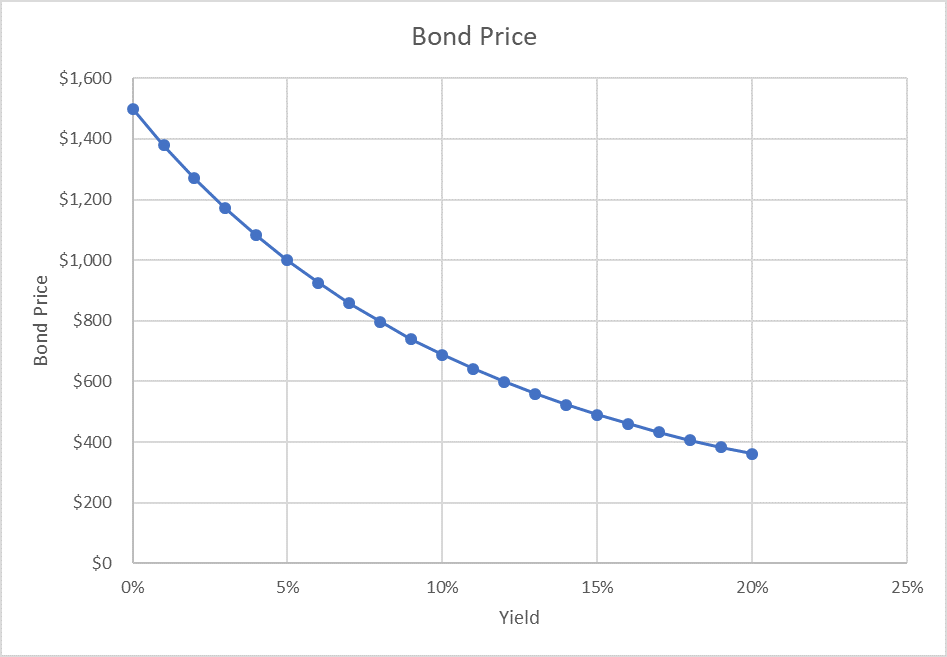
As you can see, the graph is curved which shows that the rate of change in price is different at different points on the graph. This is called convexity.
Formula
The general formula for convexity is as follows:
$$ \text{Convexity}=\frac{\text{1}}{\text{P}\times{(\text{1}+\text{y})}^\text{2}}\times\sum _ {\text{t}=\text{1}}^{\text{n}}\frac{{\rm \text{CF}} _ \text{n}\times \text{t}\times(\text{1}+\text{t})}{{(\text{1}+\text{y})}^\text{n}} $$
Where P is the bond price, y is the yield, CFn is the nth cash flow of the bond, t is the time difference between time 0 and the cash flow.
The effective convexity can be calculated using the following formula:
$$ \text{Effective Convexity}=\frac{\text{P} _ \text{i}+\text{P} _ \text{d}-\text{2P} _ \text{0}}{\text{2}\times \text{P} _ \text{0}\times{\text{deltaY}}^\text{2}} $$
Where Pi is the bond price after increase in interest rate, Pd is the bond price after a decrease in interest rate, P0 is the bond price when the yield equals the coupon rate and deltaY is the change in yield.
Percentage change in a bond price can be estimated by a combination of modified duration and the bond convexity as follows:
$$ \text{Change in Bond Price}=-\text{D}\times \text{deltaY}+\frac{{\text{deltaY}}^\text{2}}{\text{2}}\times \text{Convexity} $$
Example
If duration of the bond discussed above is 7.8, the bond price increases to $1,172 after a 2% decrease in bond yield and decreases to $858 after a 2% increase in yield, calculate the change in bond price that will occur after a 1% increase in bond yield.
We first need to calculate the convexity of the bond using the following approximation formula:
$$ \text{Effective Convexity}=\frac{\text{\$858}+\text{\$1,172}-\text{2}\times\text{\$1,000}}{\text{2}\times\text{\$1,000}\times{\text{0.2%}}^\text{2}}=\text{37.5} $$
We can work out the approximate change in bond price if the interest rates increase by 1% using the following formula:
$$ \text{Change in Bond Price}=-\text{7.8}\times\text{1%}+\frac{{\text{1%}}^\text{2}}{\text{2}}\times\text{37.5}=-\text{7.61%} $$
Based on the above percentage, the expected bond price after 1 increase in yield (from 5% to 6%) is $924 (=$1,000 × (1 – 7.61%)). Looking at the table above of the bond prices at different rates, you can see that the bond price equivalent to 6% yield is $926.
by Obaidullah Jan, ACA, CFA and last modified on