Bond Duration
Duration is a measure of interest rate risk of a debt security. It measures price sensitivity of a fixed income instrument with reference to a movement in interest rates. A higher duration means higher interest rate risk and vice versa.
Duration doesn’t simply equal the term of the fixed income security except in case of a zero-coupon bond where it equals the term of the bond. In all other cases, where there are periodic payments in addition to the final balloon payment, duration is lower than the term of the fixed income instrument.
Value of debt securities fall when the market interest rates rise simply because bond investors will prefer to invest in new debt securities offering higher stated interest rates unless the price of existing debt securities drop and vice versa. The risk resulting from sensitivity of bond prices to market interest rate is called interest rate risk. Owing to the magnifying effect of time value of money, it can be established that interest rate risk is higher for debt securities with longer term, lower coupon rates and lower yield to maturity.
Types
Macaulay duration, modified duration, effective duration and key rate duration are the main types of bond duration.
Macaulay duration
Macaulay duration simply equals the weighted average time to maturity of a debt instrument. A bond has multiple cash flows comprising of the coupon payment and the finanl maturity value each occuring on specific dates in future. Macaulay duration is calculated by finding out the time till each cash flow, weighting it by the proportion of the present value of that cash flow to the present value of all cash flows and then summing the weighted-average time. Following is the formula for Macaulay duration:
$$ \text{Macaulay Duration}=\sum _ {\text{i}}^{\text{n}}{\text{t} _ \text{i}\times\frac{{\rm \text{PV}} _ \text{i}}{\text{P}}} $$
Where ti is the time till cash flows I, PVi is the present value at time 0 of cash flow I and P is the bond price which equals the sum of all the present values.
Modified Duration
Modified duration equals Macaulay duration divided by (1 + bond yield to maturity). It is an improved version of Macaulay duration which measures the percentage price movement given a 1% movement in the bond's yield.
Following is the formula for modified duration:
$$ \text{Modified Duration}=\frac{\text{Macaulay Duration}}{\text{1}+\text{y}} $$
Where y is the bond yield.
The duration value calculated using the Macaulay duration and modified duration calculates the percentage movement in bond price if the bond's yield to maturity (which is a single rate) moves by 1%. In reality, interest rate vary with maturity i.e. interest rate that applies to a cash flow that occurs in 1 year is different than the interest rate that applies to a cash flow in 5 years. Due to this phenomenon, the best way to value a bond is to discount each cash flow using the relevant spot interest rate. Similarly, the best way to estimate price movement is measure a bond's price sensitivity to a changes in the whole term structure of interest rates. This takes us to effective duration.
Effective Duration
Effective duration is a duration measure that estimates the percentage price movement if the whole yield curve moves by 1%. It is calculated using the following formula:
$$ \text{Effective Duration}=\frac{\text{P} _ \text{d}-\text{P} _ \text{i}}{\text{2}\times \text{deltaYC}\times \text{P} _ \text{0}} $$
Where Pd is the price if the yield curve moves down i.e. when all the spot rates decrease by 1% and Pi is the price when the yield curve shifts by 1% upwards, andP0 is the base case bond price.
Duration Calculations in Excel
Excel has two functions to calculate duration: DURATION, which calculates Macaulay duration and MDURATION which calculates modified duration.
Both duration measures DURATION and MDURATION have same arguments:
DURATION(settlement, maturity, coupon, yld, frequency, [basis])
MDURATION(settlement, maturity, coupon, yld, frequency, [basis])
Settlement is the date on which duration is being calculated, maturity refers to the maturity date, coupon stands for the annual coupon rate, yld is the security’s annual yield, frequency stands for the number of coupon payments per year while [basis] is an optional argument related to day-counting method
Example
On 14 November 2017, you added the three bonds to your company’s investment portfolios: (a) a $1,000 zero-coupon bond yielding 5.1% to maturity which is 31 December 2020, (b) a $100 face-value 6% semi-annual bond maturing on 30 June 2023 and yielding 4.8% and (c) a $1,000 face value 5.5% semi-annual bond maturing on 30 June 2023 and yielding 5.8%.
As required by your risk management manual, you must calculate Macaulay duration for each bond and report it to your company’s risk manager.

As mentioned above, duration of a zero-coupon bond equals it outstanding term, while in other cases, it is less than the term of the debt instrument. Bond B is less risky than Bond C even though they have equal terms because it has higher coupon rate.
The risk manager has replied you back requesting you to calculate modified duration because Macaulay duration doesn’t consider the price sensitivity that results from changes in yield to maturity of the debt securities.
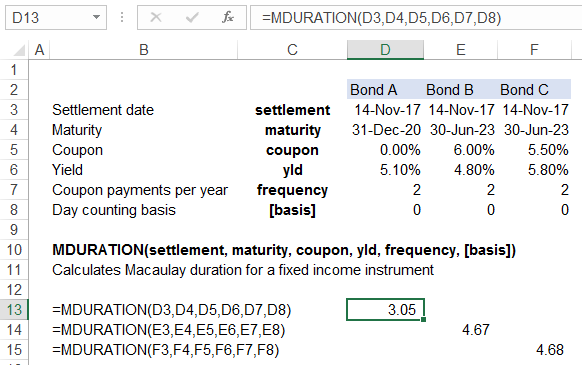
Using modified duration, our assessment of interest rate risk inherent in Bond C has dropped due to its relatively higher yield to maturity to almost cancel out Bond B’s advantage arising from comparatively higher coupon rate.
by Obaidullah Jan, ACA, CFA and last modified on