Bond Discount and Bond Premium
When the market interest rate is higher than a bond's coupon rate, the bond sells at a price lower than its face value and the difference is called bond discount. A bond premium occurs when market interest rate is lower than the bond's coupon rate and the bond sells at a price higher than the face value.
As part of the bond issuance process, the issuer sets a coupon rate keeping in view the current market interest rate and its assessment of the credit risk of the bond. However, market interest rates are volatile, and the credit risk assessment might be different from the default premium investors require in the market.
Bond Discount
If the required return on a bond is higher than the coupon rate, the demand for the bond is low and it must be issued at a price lower than the face value. This represents issuance of a bond at a discount.
Example
Let us say your company wants to raise $50 million by issued $1,000 par value bonds maturing in 10 years and paying 6% semi-annual coupon rate. If the market yield on the bond turns out to be 6.4% (which corresponds to periodic yield of 3.2%), the bond price at which your company will be able to sell each bond works out to $970.79:
| P = c × F × | 1 − (1 + r)-t | + | F |
| r | (1 + r)t |
| P = 3% × $1,000 × | 1 − (1 + 3.2%)−10×2 | + | $1,000 | = $970.79 |
| 3.2% | (1 + 3.2%)10×2 |
Where c is the periodic coupon rate (i.e. annual coupon rate divided by coupon payments per year), F is the face value of the bond, r is the periodic bond yield and t is the total number of coupon payments till maturity.
Your company will be able to raise $48.54 million (=$50 million/$1,000×$970.79). Because the face value of bonds is $50 million, you will be required to pay $50 million at maturity date. The difference of $1.46 million represent the bond discount.
Discount per Bond
= Issue Price − Face Value
= $970.79 − $1,000
= − $29.21
Total Bond Discount
= $29.21 × 50,000
= $1,460,500
The total amount of bond discount is directly proportional to the difference between the coupon rate and bond yield (i.e. market interest rate) and the time to maturity. You will be required to amortize the bond discount over the life of the bond. This will result in your interest expense to be higher than the interest payment. Your will effective interest rate will be higher than the coupon rate.
Bond Premium
If a bond’s coupon rate is set higher than the expected rate of return, the demand for bond will be higher and it can be sold at a price higher than the par value. The difference represents the bond premium.
Example
Continuing with the example above, if the annual coupon rate is 7% instead of 6% and the market interest rate is 6.4%, your bond will sell at $1,043.82 raising a total amount of $52.19 million. The amount by which the bond proceeds exceed the face value of the bond is the bond premium. It equals $2.19 million.
Premium per Bond
= Issue Price − Face Value
= $1,043.82 − $1,000
= $43.82
Total Bond Premium
= $43.82 × 50,000
= $2,191,000
The bond premium causes the interest expense to be lower than the interest payment such that the effective rate of interest is lower than the coupon rate.
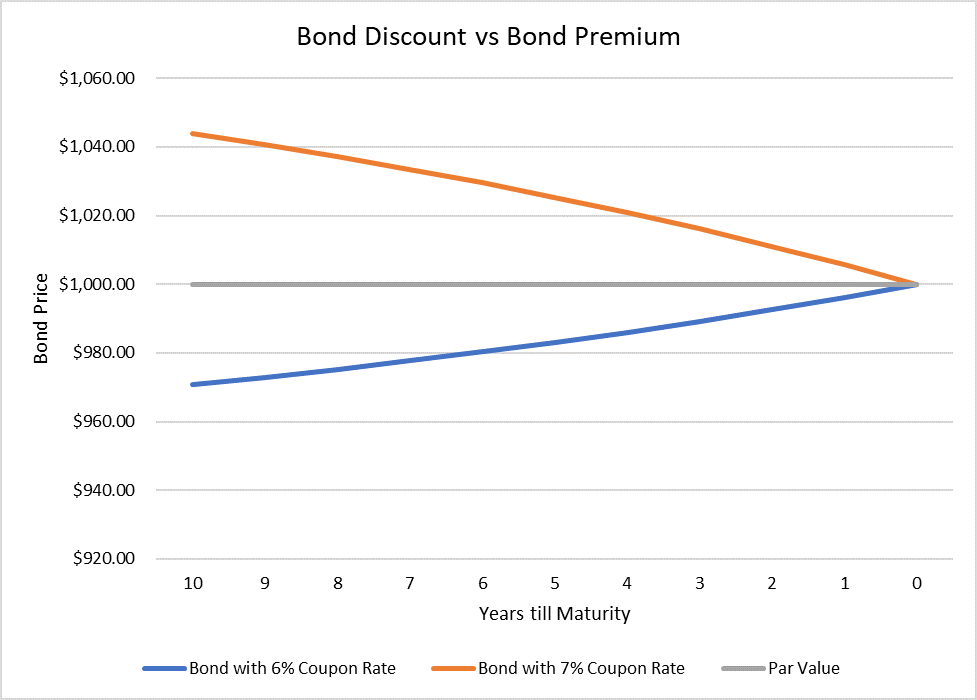
Bond discount and bond premium i.e. the difference between market price of the bond and face value decreases as the bond nears its maturity as illustrated by the following chart:
by Obaidullah Jan, ACA, CFA and last modified on