First-Degree Price Discrimination
First-degree price discrimination (also called perfect price discrimination) occurs when a producer charges each consumer his reservation price, the maximum amount that he is willing to pay, for each unit.
In order to understand (perfect) first-degree price discrimination, let’s see what happens when there is no price discrimination i.e. each customer is charged the same price. When a firm has a single price and it faces a downward-sloping demand curve, it must reduce its price for all units in order to sell one more unit. The marginal revenue of such a firm equals price adjusted for the reduction in revenue for all units due to reduction in price as shown in the equation below:
$$ \text{MR}=\text{P}+\text{Q}\times\frac{\Delta \text{P}}{\Delta \text{Q}} $$
When price decreases, ∆P is negative and marginal revenue is less than price.
In perfect (first-degree) price discrimination, the producer charges different prices for different units. It means that in order to sell one more unit, it does not need to reduce its price for units already sold. Its marginal revenue for unit x is equal to price that corresponds to unit x on the demand curve.
Example
Let’s consider a firm whose demand curve and marginal revenue curve are given by the following equations:
$$ \text{P}\ =\ \text{150}\ -\ \text{3Q} $$
$$ \text{MR}\ =\ \text{150}\ -\ \text{6Q} $$
Let’s assume that the firm’s marginal cost is $5 for first unit and it increases by $5 for each unit.
If there is no price discrimination, optimal output occurs when MR=MC. Let’s assume that in this case it occurs when output is 13 units. The demand curve tells us that the firm should set price at $111 (=150 - 3×13). Since there is no price discrimination, $111 is charged for each of the 13 units. Total revenue is $1,443 (=13×$111). Since total variable cost is $455, variable profit is $988 (=$1,443-$455).
But the demand curve tells us that the reservation price, the maximum price that consumers will pay is different from marginal revenue as shown in the table below:
| Q | Marginal Cost | Marginal Revenue | Reservation Price |
|---|---|---|---|
| 1 | 5 | 144 | 147 |
| 2 | 10 | 138 | 144 |
| 3 | 15 | 132 | 141 |
| 4 | 20 | 126 | 138 |
| 5 | 25 | 120 | 135 |
| 6 | 30 | 114 | 132 |
| 7 | 35 | 108 | 129 |
| 8 | 40 | 102 | 126 |
| 9 | 45 | 96 | 123 |
| 10 | 50 | 90 | 120 |
| 11 | 55 | 84 | 117 |
| 12 | 60 | 78 | 114 |
| 13 | 65 | 72 | 111 |
| 14 | 70 | 66 | 108 |
| 15 | 75 | 60 | 105 |
| 16 | 80 | 54 | 102 |
| 17 | 85 | 48 | 99 |
| 18 | 90 | 42 | 96 |
| 19 | 95 | 36 | 93 |
| 20 | 100 | 30 | 90 |
| 21 | 105 | 24 | 87 |
| 22 | 110 | 18 | 84 |
| 23 | 115 | 12 | 81 |
| 24 | 120 | 6 | 78 |
Reservation price for the first unit is $147 (=150 - 3×1) and so on.
Optimal Output under Price Discrimination
When there is no price discrimination and a single price is charged from each customer, the profit-maximizing output for a firm facing a downward-sloping demand curve occurs at a point at which its marginal revenue is equal to its marginal cost. But when there is price discrimination, each customer is charged a price that corresponds to the demand function, so the optimal output level occurs when the marginal cost curve intersects the demand curve (instead of the marginal revenue curve).
As the demand curve (reservation price curve) intersects marginal cost curve at close to 19 units, optimal output is 19 units and total revenue is the sum of prices charged for those 19 units
$$ \text{R}=\text{P} _ \text{1}+\text{P} _ \text{2}+\text{...}+\ \text{P} _ {\text{19}} $$
In the example above, it equals $2,280. Since marginal cost for 19 units is $950, variable profit when there is price discrimination is $1,330 (=$2,280 - $950).
It shows that by engaging in perfect price discrimination, a firm earns an additional profit of $342 (=$1,330 - $988). This arises from the firm’s ability to charge a price of $147 for the first unit, $144 for the second unit and so on instead of a single price of $111 for each unit and due to increase in the optimal output.
The graph below shows perfect price discrimination at work.
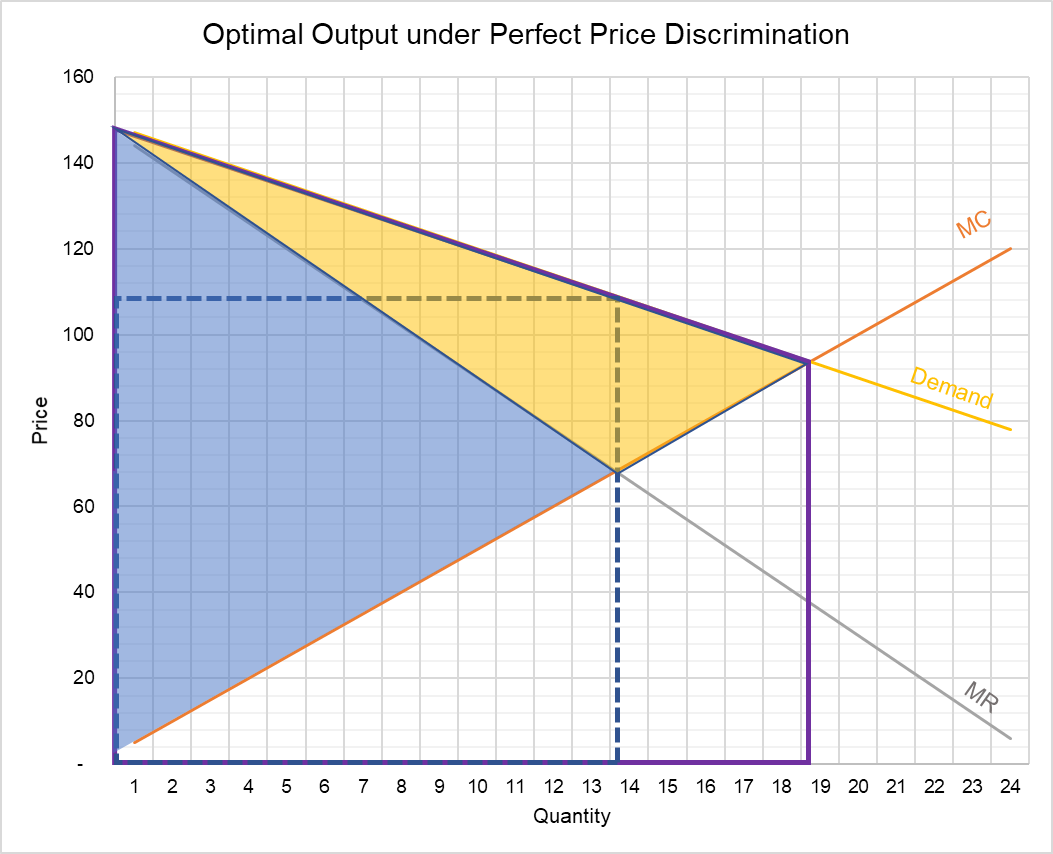
The rectangle with blue dashed line shows optimal output and price when there is no price discrimination and the solid purple figure shows optimal output and total revenue when there is perfect price discrimination.
The light-blue triangle shows (variable) profit when there is no price discrimination while the yellow triangle shows the additional profit that has been possible due to perfect price discrimination.
When price is $111, the difference between reserve price and the market price represents consumer surplus. Through perfect price discrimination, the producer has effectively captured all of the consumer surplus.
Imperfect First-Degree Price Discrimination
In order to be able to charge each customer the maximum amount, firms must have complete information about its customers and the customers mustn't be able to sell the product to each other. In most cases, perfect information about customer reservation prices is not available. This is why perfect price discrimination is very rare. In reality, reservation price information about different groups of customers may be available and imperfect first-degree price discrimination can be applied to maximize profit.
by Obaidullah Jan, ACA, CFA and last modified on