Third-Degree Price Discrimination
Third-degree price discrimination (also called group price discrimination) occurs when a firm divides its customers into two or more groups based on their price elasticity of demand and charges them different prices.
Third-degree price discrimination is the most common type of price discrimination because classifying customers into a few groups is easier for a firm than knowing the reservation price, the maximum amount that consumers are willing to pay, of each unit of its output.
Following are a few real-life examples of third-degree price discrimination.
- Hardcover and paperback version of a book: Publishers typically release hardcovers first and price them at a premium to paperbacks which are released after a significant delay. They do this because they want to charge higher price to people who are more eagerly waiting for a book and lower price to people who have a higher elasticity of demand.
- Low price editions of textbooks: Many textbooks have a special edition which is sold in developing countries. Even though in most cases the special edition differs only in their covers, it is priced significantly lower than the edition published in developed countries. It is because people in developing countries are more price-sensitive.
- Airline tickets: People who book tickets close to their travel date and/or without a weekend stay are charged a higher price because they have inflexible schedules and low elasticity of demand. People who book tickets well in advance are charged a lower fare because their demand is more elastic.
Optimal Output under Third-Degree Price Discrimination
Let’s consider AryaSoft, a developer of a premium movie-editing software, which engages in third-degree price discrimination based on intended use of its software. The inverse demand functions and associated marginal revenue functions for personal and commercial consumers are as follows:
$$ \text{P} _ \text{P}=\text{50}\ -\ \text{5Q} _ \text{P} $$
$$ {\text{MR}} _ \text{P}=\text{50}\ -\ \text{10Q} _ \text{P} $$
$$ \text{P} _ \text{C}=\text{75}\ -\ \text{15Q} _ \text{C} $$
$$ {\text{MR}} _ \text{C}=\text{75}\ -\ \text{30Q} _ \text{C} $$
Where Q is in thousands of copies sold.
The firm’s marginal cost (MC) is fixed at $3.
The profit-maximizing output for each segment occurs where the marginal revenue of the segment equals the marginal cost. The overall profit is maximized when the sum of profit from both segments is maximized.
The profit from personal segment is maximized when MRP equals $3:
$$ \text{50}\ -\ \text{10Q} _ \text{P}=\text{3} $$
$$ \text{Q} _ \text{P}=\text{4.7 thousand} $$
This corresponds to a price of $26.5:
$$ \text{P} _ \text{P}=\text{50}\ -\ \text{5}\times\text{4.7}=\text{26.5} $$
Similarly, the profit-maximizing output and price in the commercial segment is 2.4 thousand and $39 respectively.
$$ \text{75}\ -\ \text{30Q} _ \text{C}=\text{3} $$
$$ \text{Q} _ \text{C}=\text{2.4 thousand} $$
$$ \text{P} _ \text{C}=\text{75}\ -\ \text{15}\times\text{2.4}=\text{\$39} $$
Graph
The following graph plots the profit-maximizing output in both segments.
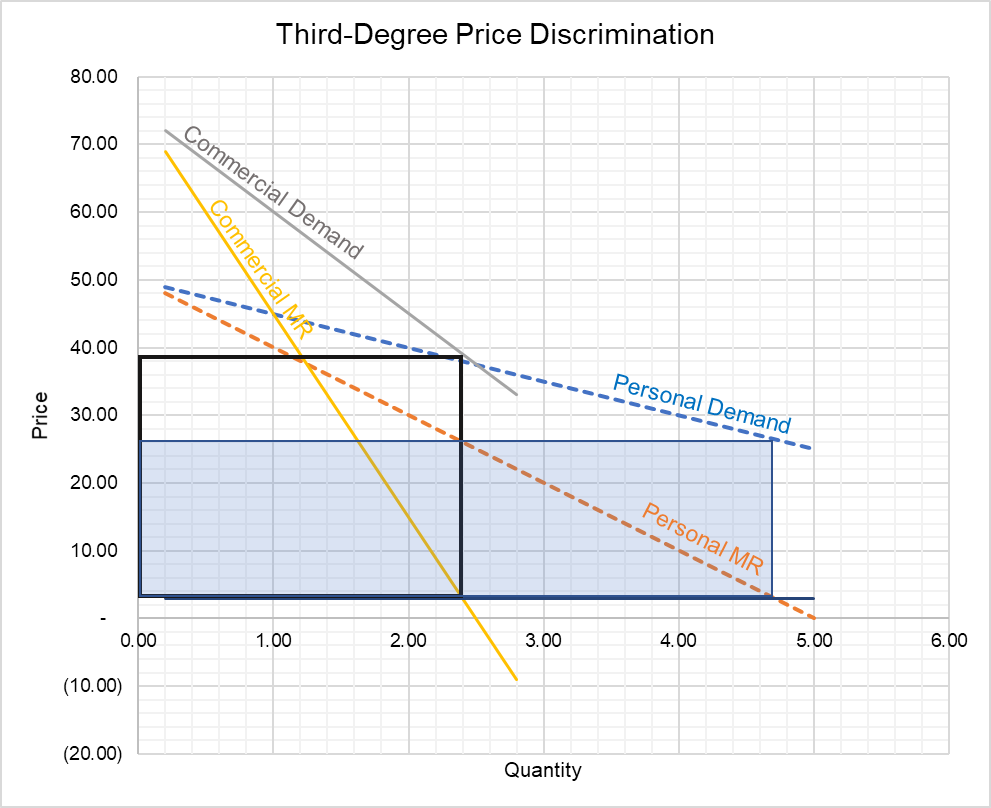
The commercial demand curve is steeper than the personal demand curve precisely because commercial segment has lower elasticity of demand.
The blue-shaded rectangle shows variable profit from the personal segment and the rectangle with black borders shows profit from the commercial segment.
by Obaidullah Jan, ACA, CFA and last modified on