Marginal Revenue
Marginal revenue is the incremental revenue generated from each additional unit. It is the rate at which total revenue changes. It equals the slope of the revenue curve and first derivative of the revenue function.
Economists are interested in finding a firm’s marginal revenue because its profit maximization output occurs at a point at which its marginal revenue equals its marginal cost. It is because when the marginal revenue is more than the marginal cost, the firm has a potential to increase profit because an additional unit will fetch net profit because MR minus MC is positive. On the other hand, if the marginal revenue is less than the marginal cost, the firm is making loss on the marginal units and it can cut losses by reducing its output until the marginal revenue covers its marginal cost.
Marginal revenue equals change in total revenue (∆TR) divided by change in total output (∆Q)
$$ {\rm \text{MR}} _ \text{Q} = \frac{\Delta \text{TR}}{\Delta \text{Q}} $$
Marginal revenue can also be worked out from a firm’s revenue function by differentiating it with respect to Q.
Marginal Revenue of Perfectly-Competitive Firm
Let’s consider Snow Inc., a perfectly-competitive firm. Its total revenue of Q units is 300Q where $300 is the price. Marginal revenue is this case can be calculated as follows:
$$ \text{MR}=\frac{\text{dTR}}{\text{dQ}}=\frac{\text{d}(\text{300Q})}{\text{dQ}}=\text{300} $$
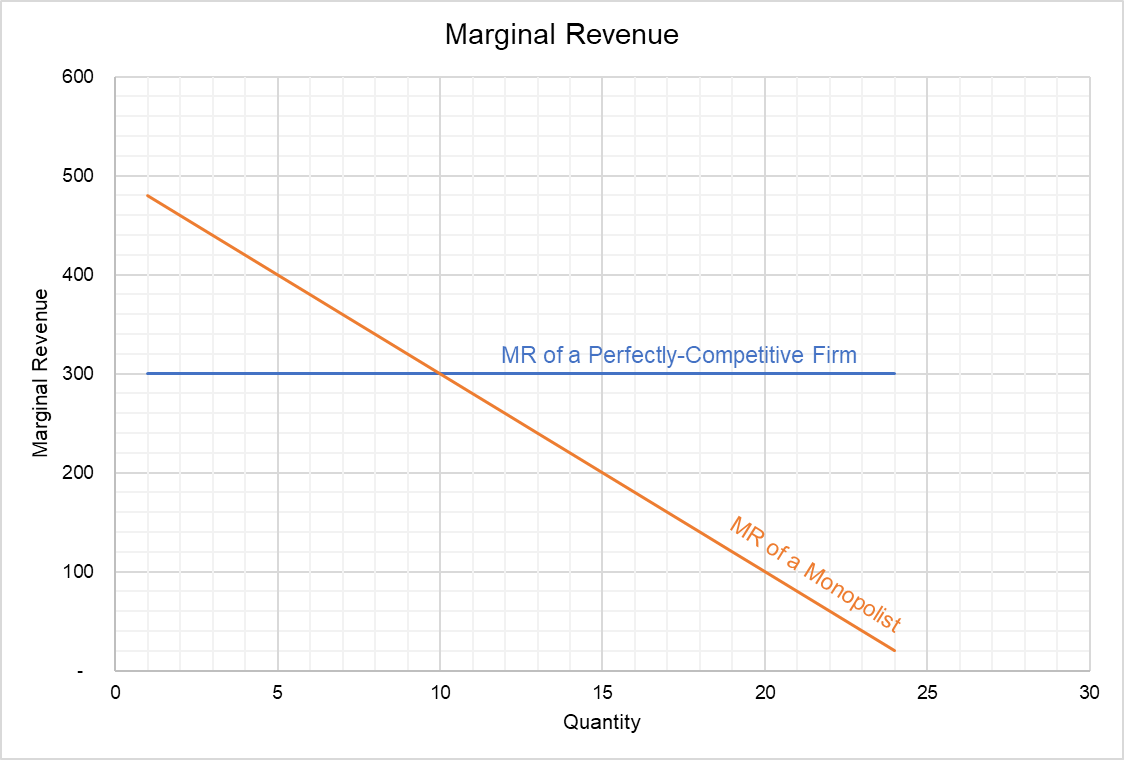
It shows that the marginal revenue of a perfectly-competitive firm is constant, and its marginal revenue curve is a horizontal line.
Marginal Revenue of a Monopolist
In case of a monopolist, the marginal revenue is not necessarily equal to the price because he faces a downward sloping demand function which results in a downward-facing marginal revenue curve. Total revenue of a monopolist increases with decreasing rate because in order to increase its total revenue, the monopolist must reduce its price. The change in revenue is the combined result of the quantity effect and the price effect. The revenue increases due to increase in quantity but decreases due to decrease in price.
Let’s consider Sparrow, Inc., a monopolist. Its total revenue function is given by the following equation:
$$ \text{TR}=\text{500Q}\ -\ \text{10Q}^\text{2} $$
The marginal revenue function can be derived by taking the first derivative of the TR function:
$$ \text{MR}=\frac{\text{dTR}}{\text{dQ}}=\text{500}\ -\ \text{20Q} $$
A marginal revenue curve is a graphical representation of the relationship between marginal revenue and quantity. If we plot the marginal revenue curves for a Snow and Sparrow, it will look like as follows:
by Obaidullah Jan, ACA, CFA and last modified on