Excel INTRATE Function
INTRATE is an Excel function that calculates the annual effective interest rate earned on a fully invested security. A fully invested security is the one in which you do not receive any cash flows before maturity instead your interest income results from the difference between the redemption value of your security and your investment.
INTRATE function can be used to calculate interest rate on securities that pay interest at maturity such has promissory notes, certificates of deposit, etc.
INTRATE function is different from the RATE function because RATE function calculates the periodic nominal interest rate. INTRATE essentially calculates the annual simple interest rate.
Syntax
INTRATE syntax is:
INTRATE(settlement, maturity, investment, redemption, [basis]
Settlement refers to the settlement date, the date on which you invest in the security.
Maturity is the maturity date of the security, i.e. the date on which you will receive the redemption value.
Investment means the actual amount of your investment in the security at the settlement date.
Redemption refers to the amount you receive on maturity date.
[Basis] is an optional argument specifying the day-counting method.
The back-end formula Excel uses for the function is:
$$ \text{INTRATE}\ =\ \frac{\text{redemption}-\text{investment}}{\text{investment}}\times\frac{\text{days in a year}}{\text{days between maturity and settlement}} $$
The [basis] argument tells Excel whether to use 30/360 days or actual/actual days or any other day-counting method.
Example
You invested $20,000 in a security issued by your university’s fund on 1 January 2017 that pays $30,000 on 31 December 2020. Calculate the interest rate that you earn on the security.
You can use Excel INTRATE function to get a rate of 12.50% per annum.
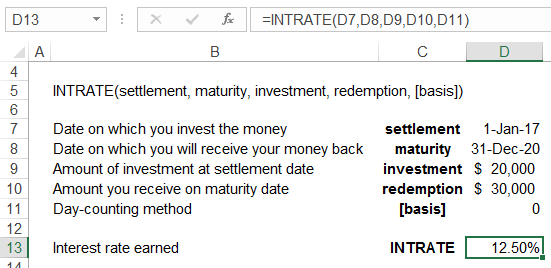
INTRATE always returns the annual rate.
The above calculation can be replicated manually as follows:
$$ \text{INTRATE}\ =\ \frac{\text{\$30,000}-\text{\$20,000}}{\text{\$20,000}}\times\frac{\text{360}}{\text{1,440}}=\text{12.5%} $$
by Obaidullah Jan, ACA, CFA and last modified on