Excel RATE Function
RATE is an Excel function that calculates the interest rate that applies to a system of present value, periodic equidistant equal cash flows and/or a future value over a specific number of periods. I can be used to calculate the interest rate that equates the discounted value of a single sum of future cash flows and/or the discounted value of stream of equidistant equal future cash flows to a given present value. Alternatively, it can be used to calculate the interest rate at which a single sum of cash flow today and/or a stream of periodic equidistant equal cash flows accumulate to a given future value.
RATE is an iterative calculation which means that Excel tries different values until it arrives at a value that best fits the time value of money equation.
RATE essentially returns the value of RATE in either of the following equation:
$$ \text{PV}=\text{PMT}\ \times\frac{\text{1}-{(\text{1}+\text{RATE})}^{-\text{NPER}}}{\text{RATE}}+\frac{\text{FV}}{{(\text{1}+\text{RATE})}^{\text{NPER}}} $$
$$ \text{FV}=\text{PV}\times{(\text{1}+\text{RATE})}^{\text{NPER}}+\text{PMT}\times\frac{{(\text{1}+\text{RATE})}^{\text{NPER}}-\text{1}}{\text{RATE}} $$
Finding the value of RATE using algebraic manipulation of the above equations is hard. We must use the trial and error method using the time value of money tables or use Excel RATE function.
Syntax
RATE function has the following syntax:
RATE(nper, pmt, pv, [fv], [type])
Arguments within square brackets are optional. If there is no PV value, there must be an FV value to allow the function to proceed.
NPER stands for the total number of compounding periods, it equals the product of total number of years and number of compounding periods per year.
PMT stands for the periodic equal cash flow that occurs after every fixed interval of time.
PV stands for a single sum of value today i.e. at t=0.
FV stands for a single sum of value at t=NPER.
[type] argument specifies whether the cash flows occur at the end of each period or at the beginning. It has two values: 0 where the cash flows occur at the period end (simple annuity) or 1 where the cash flows occur at the start of the period (annuity due). The default value is 0 which means that if no value is entered in [type] argument, Excel assumes that cash flows occur at the end of each period.
Example
Your mom gave you $18,000 on your graduation and you promised her you will get a new car with that money. A car dealer offered you two options: pay $18,000 today or pay $2,000 every six months for next 5 years followed by a single payment of $5,000 at the end of fifth year. Before you could figure out which option is better, a class mate of yours, who runs a college fund that loans out money to people who are admitted to the college’s MBA program and need student loans, asked you to invest the money in the fund to get $30,000 at the end of fifth year. Let’s find out how can Excel get you out of this dilemma.
You need to find out if the rate offered by the college fund is higher than the interest rate embedded in the car lease. If the investment rate is higher than the interest rate, you should put the money in the fund and take out the lease, otherwise you should just pay cash to get the car. You can calculate the rates using Excel RATE function as illustrated below:
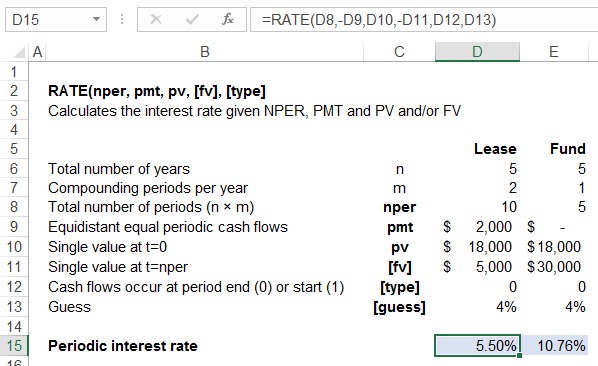
Looking at the formula bar in case of lease rate calculation, please notice that we entered lease outflows as negative values and the t=0 value as positive. This is because the sign of cash flows matters in any time value of money system. Where the direction of cash flow is opposite, the signs must be opposite too and vice versa.
Result of the RATE function is the periodic rate which must be multiplied by the number of compounding periods per year (m) to get the annual percentage rate. In case of lease, the annual percentage rate is 11% (=5.50% × 2). In case of investment, the annual percentage rate is 10.76% because there is one compounding period per year.
You should buy the car with $18,000 in cash because the annual rate that you are paying on the lease is higher than the rate that you can get on the investment.
by Obaidullah Jan, ACA, CFA and last modified on