Excel PMT Function
PMT is an Excel function that finds out the total constant periodic payment of a stream of cash flows at a specific interest rate for a specific duration. By default, the function assumes that the constant cash flow occurs at the period end. However, it can be used to find out the amount of periodic cash flow where it occurs at the start of each period.
If PV is given, PMT function calculates PMT based on the following equation:
$$ \text{PV}=\text{PMT}\times\frac{\text{1}-({\text{1}+\text{RATE})}^{-\text{NPER}}}{\text{RATE}} $$
Where FV is given, PMT function calculates PMT based on the following equation:
$$ \text{FV}=\text{PMT}\times\frac{({\text{1}+\text{RATE})}^{\text{NPER}}-\text{1}}{\text{RATE}} $$
Where both PV and FV are given, PMT can be worked out using either of the following equation:
$$ \text{PV}=\text{PMT}\times\frac{\text{1}-({\text{1}+\text{RATE})}^{-\text{NPER}}}{\text{RATE}}+\frac{\text{FV}}{{(\text{1}+\text{RATE})}^{\text{NPER}}} $$
or
$$ \text{FV}=\text{PV}\times\left(\text{1}+\text{RATE}\right)^{\text{NPER}}+\text{PMT}\times\frac{({\text{1}+\text{RATE})}^{\text{NPER}}-\text{1}}{\text{RATE}} $$
Syntax
PMT function has the following syntax:
PMT(rate, nper, pv, [fv], [type])
The values in square brackets are optional while all other values are mandatory.
Rate is the periodic interest rate applicable to the stream of cash flows i.e. a mortgage. The rate entered must correspond to the length of each payment period i.e. if each payment is after one year, you need to enter the yearly interest rate; and if the period is a quarter, you need to enter the quarterly interest rate (=annual percentage rate/4).
NPER is the number of periods in the cash flow stream. It should be entered in units of time that corresponds to the payment duration. If each periodic payment is after 1 year, NPER should be entered in years.
PV is the present value of the cash flow stream.
FV is an optional value. It represents the future value of the loan or investment. It is useful in case of cash flow stream that have a large balloon payment at the end, for example a bond or some leases.
[type] is an optional value with binary input (i.e. 0 or 1). You need to enter 0 when the cash flow stream is an annuity i.e. each payment occurs at the end of the period and 1 when the cash flow stream represents and annuity due i.e. when each payment occurs in advance i.e. at the start of the period. The default value is 0, so if you don’t enter anything, Excel calculates periodic cash flow assuming each cash flow occurs at the end of the period.
Example
We will learn how to calculate monthly payment on a mortgage.
Let’s say you want to take out a 15-year mortgage for $300,000 at 4% per annum with payments due at the end of each month. After the 15th year, you have zero balance on the mortgage. You need to find your monthly mortgage payment.
Your formula will look like as follows:
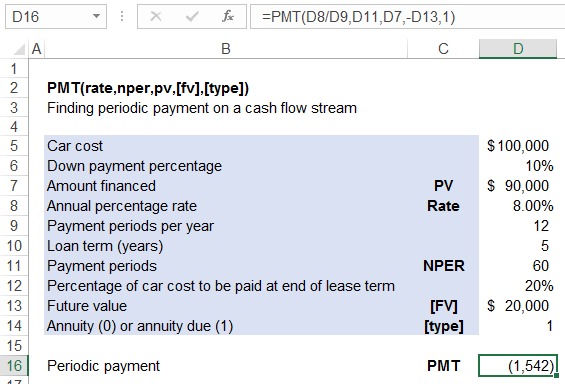
As you can see in the Formula Bar, we entered D6/D7 for the rate argument because since payment periods are in quarters, we need to include the quarterly rate. The periodic payment result that we got has a negative sign, it is because the cash flow directions are opposite. The initial present value was a cash inflow and we need to make the periodic payments which are outflows.
Let’s learn how to use the formula in a situation when there is a FV and when payments are due in advance. Let’s assume you lease out a car that costs $100,000 at 8% per annum and 10% down-payment. The lease term is five years with monthly payments due at the start of each month. You always change cars after 5 years and you plan to sell the car at 20% of its cost after the 5 years and use it to repay the lease obligation. Now, you need to calculate such a monthly payment that will reduce your lease obligation balance such that exactly the leas payable balance at the end of 5th year equals 20% of the car cost.
Please follow the snapshot below for calculation:
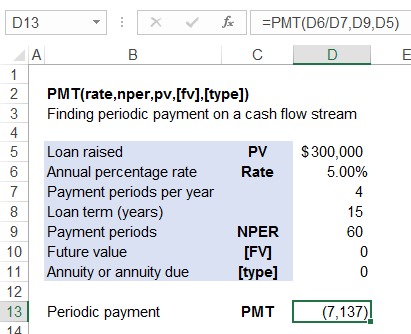
You are paying 10% down payment, so amount financed is $90,000. If you look at the formula, we have used monthly interest rate (=8%/12), NPER of 60 (=5 × 12), present value with a negative sign of $90,000, future value with a positive sign of $20,000 and value of 1 for the type argument because the monthly payments occur at the start of the period. Sign is extremely important in all time value of money functions. We used a positive sign with PV argument because at t=0 we are receiving leased asset equal to the present value of lease payments. However, at the end of lease term, we must pay $20,000 lump sum, so FV sign must be exact opposite of the PV cash flow sign, i.e. negative. The result of the function is also negative which means it is an outflow.
by Obaidullah Jan, ACA, CFA and last modified on