Amortizing Bond vs Bullet Bond
An amortizing bond is a bond that pays both principal and interest through periodic payments while the bullet bond is a bond that pays interest through periodic payments and the principal amount at maturity through a single payment.
The principal balance of the amortizing bond is reduced with each payment such that it becomes zero at maturity, but the principal balance of the bullet bond stays the same throughout the life of the bond. A fully-amortized bond does not require any lump sum principal repayment at maturity, but a bullet bond must make the full principal repayment at the maturity date. A partially-amortized bond can also be issued which pays only a certain portion of the principal through periodic payments. Such a bond requires a balloon payment at the maturity date. Consequently, the periodic payments required on an amortizing bond are higher than periodic payments to be made on a bullet bond of the same par value and life.
Majority of the bonds are bullet bonds. They pay periodic fixed coupon payments semiannually based on a fixed or floating coupon rate and the final principal amount at maturity. The coupon rate is determined keeping in view the market interest rates and the credit risk of the bond. The price of a bullet bond equals the present value of the annuity of coupon payments plus the present value of the maturity payment. The price of a bullet bond hovers around the par value unless there is a default.
Amortizing bond price also equal the present value of its future cash flows but because the principal balance is reduced, the bond price falls with each payment.
Example
Your company wants to raise $100 million. It is considering whether to issue a bullet bond or an amortizing bond. The bond will have a term of 5 years and will make annual payments. If the market interest rate is 6% and the coupon rate will be set at 6%, create a schedule of bond payments required under both options.
In case of the bullet bond, you will be required to pay five interest payments at the end of each of the 5 years each amounting to $6 million (=$100 million × 6%) and a final maturity payment equal to the face value of the bond i.e. $100 million.
In case of the amortizing bond, your annual payments can be worked out using the following formula for present value of an (ordinary) annuity:
| $100 million = PMT × | 1 − (1 + 6%)-5 |
| 6% |
Payment at the end of each year will amount to $23.74 million. The following schedule shows the amortizing bond cash flows, interest payment and principal payment (all amount in millions):
| Year | Opening Bond Principal |
Total Payment |
Interest Payment |
Principal Payment |
Closing Bond Principal |
|---|---|---|---|---|---|
| P | C | I = P×6% | R=C-I | CP=P-R | |
| 0 | 100.00 | ||||
| 1 | 100.00 | 23.74 | 6.00 | 17.74 | 82.26 |
| 2 | 82.26 | 23.74 | 4.94 | 18.80 | 63.46 |
| 3 | 63.46 | 23.74 | 3.81 | 19.93 | 43.52 |
| 4 | 43.52 | 23.74 | 2.61 | 21.13 | 22.40 |
| 5 | 22.40 | 23.74 | 1.34 | 22.40 | - |
In case of the bullet bond, the interest expense each year is constant but in an amortizing bond, the interest expense decreases with each payment and the principal repayment component increases over time as illustrated by the following chart.
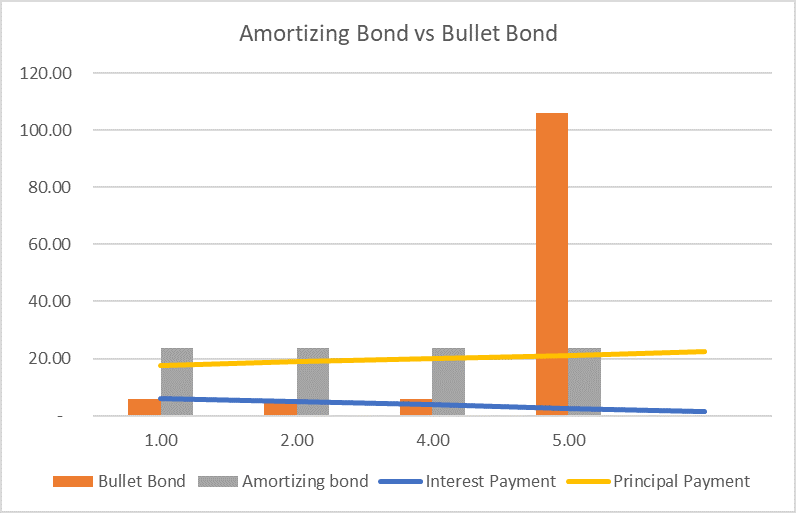
The price of an amortizing bond equals the present value of the remaining bond payments. For example, at the end of 2nd year, if the market interest rate is 5.5%, the principal bond value will be $64.05 million:
| P = $23.74 M × | 1 − (1 + 5.5%)(5-2) | = $64.05 M |
| 5.5% |
The corresponding price of the bullet bond after 2 years will be:
| P = $6 M × | 1 − (1 + 5.5%)(5-2) | + | $100 M | = $101.35 M |
| 5.5% | (1 + 5.5%)(5-2) |
by Obaidullah Jan, ACA, CFA and last modified on