Scatter Graph Method
Scatter graph method is a graphical technique of separating fixed and variable components of mixed cost by plotting activity level along x-axis and corresponding total cost (i.e. mixed cost) along y-axis. A regression line is then drawn on the graph by visual inspection. The line thus drawn is used to estimate the total fixed cost and variable cost per unit. The point where the line intercepts y-axis is the estimated fixed cost and the slope of the line is the average variable cost per unit. Since the visual inspection does not involve any mathematical testing therefore this method should be applied with great care.
Procedure
Step 1: Draw scatter graph
Plot the data on scatter graph. Plot activity level (i.e. number of units, labor hours etc.) along x-axis and total mixed cost along y-axis.
Step 2: Draw regression line
Draw a regression line over the scatter graph by visual inspection and try to minimize the total vertical distance between the line and all the points. Extend the line towards y-axis.
Step 3: Find total fixed cost
Total fixed is given by the y-intercept of the line. Y-intercept is the point at which the line cuts y-axis.
Step 4: Find variable cost per unit
Variable cost per unit is equal to the slope of the line. Take two points (x1,y1) and (x2,y2) on the line and calculate variable cost using the following formula:
$$ \text{Variable Cost per Unit} \\= \text{Slope of Regression Line} \\= \frac{\text{y} _ \text{2} - \text{y} _ \text{1}}{\text{x} _ \text{2} - \text{x} _ \text{1}} $$
Example
Company α decides to use scatter graph method to split its factory overhead (FOH) into variable and fixed components. Following is the data which is provided for the analysis.
| Month | Units | FOH |
| 1 | 1,520 | $36,375 |
| 2 | 1,250 | 38,000 |
| 3 | 1,750 | 41,750 |
| 4 | 1,600 | 42,360 |
| 5 | 2,350 | 55,080 |
| 6 | 2,100 | 48,100 |
| 7 | 3,000 | 59,000 |
| 8 | 2,750 | 56,800 |
Solution:
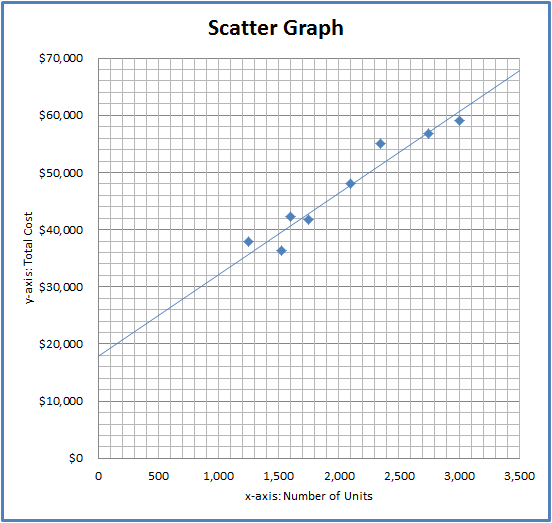
Fixed Cost = y-intercept = $18,000
Variable Cost per Unit = Slope of Regression Line
To calculate slop we will take two points on line: (0,18000) and (3500,68000)
Variable Cost per Unit = (68000 − 18000) ÷ (3500 − 0) = $14.286
by Irfanullah Jan, ACCA and last modified on