Cost-Volume-Profit Analysis
Cost-Volume-Profit (CVP) analysis is a managerial accounting technique which studies the effect of sales volume and product costs on operating profit of a business. It shows how operating profit is affected by changes in variable costs, fixed costs, selling price per unit and the sales mix of two or more products.
CVP analysis is concerned with identification of a company's fixed costs, its variable cost per unit, the price of its product and using this data to work out the following measures:
- Contribution margin: The difference between a company's total revenue and total variable costs. It is the amount that sales contribute towards fixed costs and profit.
- Contribution margin per unit: The difference between sales price and variable cost per unit.
- Contribution margin ratio: The ratio of contribution margin to total revenue.
- Break-even point: The sales volume (in units and dollars) at which the company is neither making a loss nor earning any profit.
- Target income sales: The sales level necessary to achieve a target income.
- Margin of safety: The percentage (or dollars) by which a company's sales volume exceeds its break-even point.
The most critical input in CVP analysis is the relationship between different costs and volume i.e. the categorization of costs into fixed and variable categories.
CVP Analysis Equation
The fundamental cost-volume-profit relationship can be derived from profit equation:
Profit = Revenue – Fixed Costs – Variable Costs
Where profit is PR, revenue equals the product of price per unit P and sales volume in units Q, fixed costs FC are constant and total variable costs equal the product of units sold Q and variable cost per unit V, the following equation is a more elaborate representation of CVP relationships:
PR = Q × P - Q × V - FC
This is the most fundamental equation which can be used to work many CVP numbers.
For break-even point, we need to set PR ad 0 and solve for Q and we get:
Break-even Q = FC ÷ (P – V)
It shows that break-even point can be calculated by dividing fixed cost by the contribution margin per unit.
Contribution Margin Equation Approach
The CVP equation discussed above can also be expressed in terms of contribution margin of the product:
PR = Q × P - Q × V - FC
PR = Q × (P – V) – FC
(P – V) in the equation above is contribution margin per unit.
CVP Graph
CVP relationship can also be expressed in the form of a graph called CVP graph:
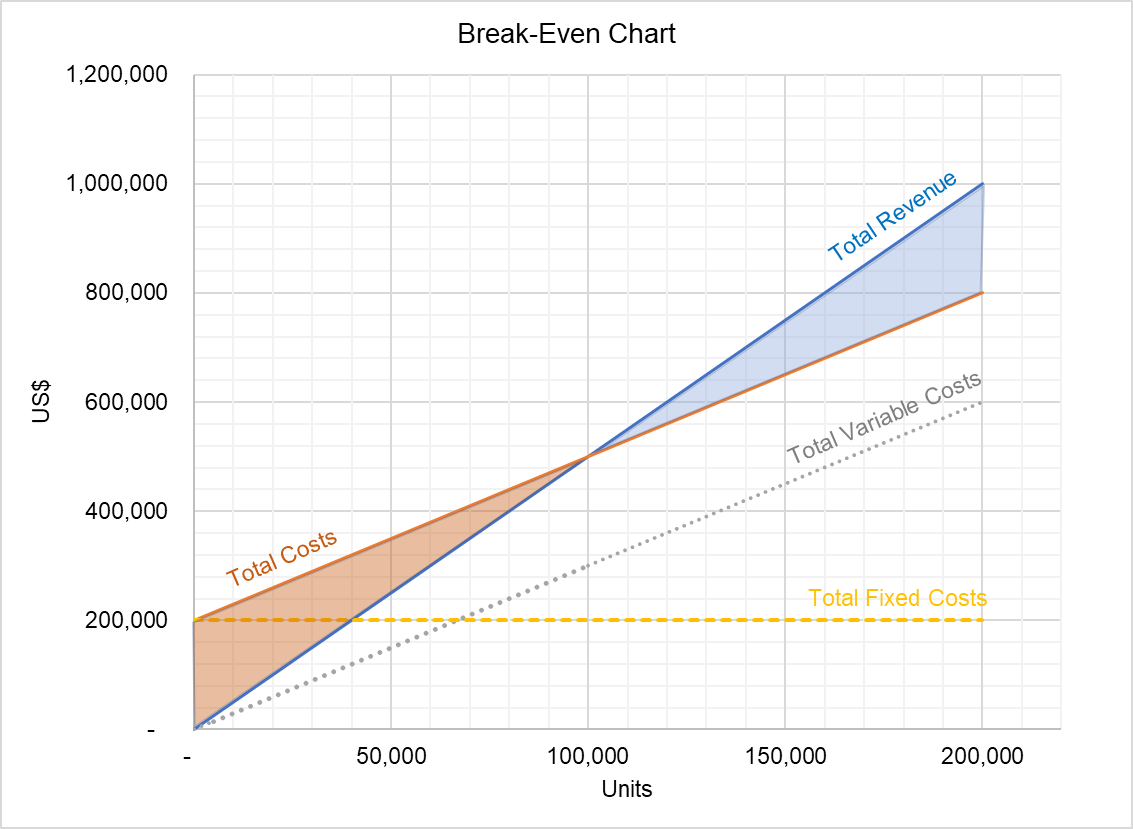
The graph above shows the relationship between total revenue and total costs. The area between the two lines below the break-even point represents losses and the area above the breake-even point shows the volume of total profit. This graph can be used to identify profit at different output levels.
CVP Analysis Assumptions
Even though CVP analysis is a useful management accounting tools, its conclusions are valid only when the following assumptions hold:
- All cost can be categorized as variable or fixed. For this purpose, mixed costs are bifurcated into variable and fixed components using techniques such high-low method, scatter graph method and regression analysis.
- Sales price per unit, variable cost per unit and total fixed cost are constant. This assumption is problematic due to existence of economies of scale, increasing/decreasing returns to scale and learning curve effect.
- All revenues and cost have a linear relationship with volume.
- The sales mix of a company remains constant.
by Irfanullah Jan, ACCA and last modified on