Mixed Costs
Mixed costs (also called semi-variable costs) are costs that have both fixed and variable components. The fixed element doesn’t change with change in activity level at all and the variable component changes proportionately with activity.
Fixed cost, variable cost and mixed cost are three categories of costs with respect to cost behavior, i.e. the relationship between total cost and output in the relevant range. A mixed cost differ from fixed cost in that the total mixed cost changes while the fixed cost remain constant. Similarly, mixed cost differs from variable cost in that the per-unit change in variable cost is fixed while the per-unit change in mixed cost decreases as output increases.
A mixed cost can be bifurcated into fixed and variable elements using high-low method, scatter-graph method and least-squares regression.
Typical real-life examples of mixed costs include:
- Employee benefits: companies typically pay fixed base salaries and variable bonuses and commissions depending on employee performance.
- Telecommunications expense: phone companies typically charge a fixed amount regardless of actual usage plus a variable component which depends on usage.
- Car rental expense: car rent expense has a certain base fare and a variable fare which depends on actual distance travelled and time spent on the trip.
- Legal fees and other charges: some law firms charge a fixed retainership fee plus a variable fee depending on the actual legal cases.
- Audit fee: audit firms charge a fixed fee plus a variable component which reflects the time spent by the audit team plus out-of-pocket expenses.
Formula
A mixed cost can be represented by the following equation:
TMC = FC + v × Q
Where TMC is the total mixed cost, FC is the fixed component, vc is the variable cost per unit and Q is the output level.
Example
Your Uber ride is typically a mixed cost which can be represented by the following simplified equation:
T = BF + R × D
Where T is the total trip cost, BF is the base fare which is the same whether you travel 0.5 km or 20 km. R is the variable charge per kilometer for distance and D represents distance in kilometers.
Let’s assume that the base fare is $5, variable cost per km is $2, your total bill for 0.01 kilometers, 10 kilometers and 30 kilometers would be as follows:
T(0) = $5 + 2 × 0.01 ≈ $5
T(5) = $5 + 2 × 5 = $15
T(15) = $5 + 2 × 15 = $35
Plotting the above data gives us the following graph:
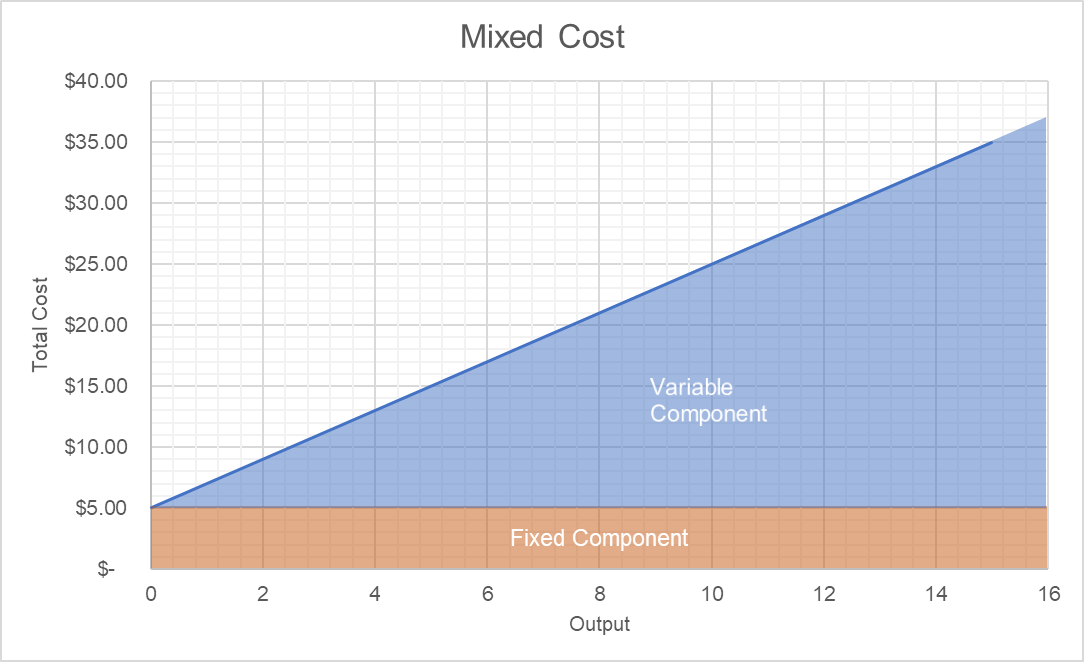
The red-shaded area shows the fixed component which stays same at all output levels (0 – 16) and the blue-shaded area shows the variable component which increases with increase in output.
by Obaidullah Jan, ACA, CFA and last modified on