Binomial Option Pricing Model
Binomial option pricing model is a risk-neutral model used to value path-dependent options such as American options. Under the binomial model, current value of an option equals the present value of the probability-weighted future payoffs from the options.
It is different from the Black-Scholes-Merton model which is most appropriate for valuing path-independent options.
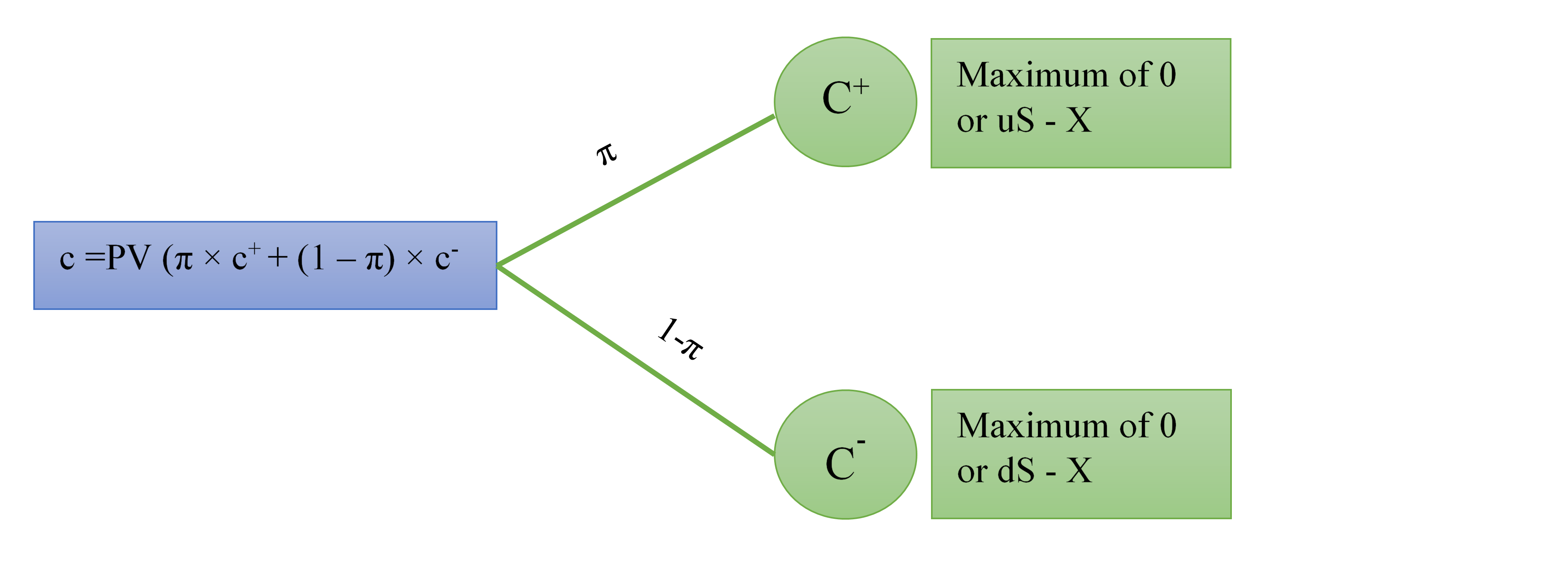
Let’s consider a call option, an option which entitles the holder to purchase the underlying (stock, bond, etc.) whose current price is referred to as S at the exercise price X. At any point of time, the underlying can have two price movements: either an up move or a down move. In case of the up move, the ratio of the new price S+ to S is called the up-factor u. Similarly, in case of a down move, the ratio of the new price S- to S is called the down-factor d. The call option is in-the-money when the spot price of the underlying is higher than the exercise price of the option. In case of an up movement, the payoff from the call option (c+) equals max(0,uS – X) i.e. the maximum of 0 or the difference between new spot price and exercise price. On the other hand, in case of a down movement, the call option payoff (c-) equals the higher of 0 or (dS – X). The binomial model effectively weighs the different payoffs with their associated probability and discounts them to time 0.
Binomial Tree
Binomial model is best represented using binomial trees which are diagrams that show option payoff and value at different nodes in the option’s life. The following binomial tree represents the general one-period call option.
Formula
The call option value using the one-period binomial model can be worked out using the following formula:
$$ \text{c}=\frac{\pi\times \text{c}^++(\text{1}-\pi)\times \text{c}^-}{\text{1}+\text{r}} $$
Where π is the probability of an up move which in determined using the following equation:
$$ \pi=\frac{\text{1}+\text{r}\ -\ \text{d}}{\text{u}\ -\ \text{d}} $$
Where r is the risk-free rate, u equals the ratio the underlying price in case of an up move to the current price of the underlying and d equals the ratio of the underlying price in case of a down move to the current price of the underlying.
The payoff pattern of a put option, an option that entitles the holder to sell the underlying at the exercise price is exactly opposite, i.e. its value in case of an up (p+) or down movement (p-) in the underlying price S is max(X-uS,0) and max(X-dS,0) respectively. The value of a put option using single-period binomial model can be calculated using the following formula:
$$ \text{p}=\frac{\pi\times \text{p}^++(\text{1}-\pi)\times \text{p}^-}{\text{1}+\text{r}} $$
In case of a multi-period binomial model, you just need to add additional stages in the calculation as illustrated in the example below. The terminal pay-off of a call or put option after different price movements can be worked by multiplying the up and down factor for every price move. The following table summarizes the different pay-off situations
| Period 1 Price | Period 2 Price | Underlying Price at Expiration | Call Option Payoff | Put Option Payoff |
|---|---|---|---|---|
| Up | Up | uuS | Max(uuS-X,0) | Max(X- uuS,0) |
| Up | Down | udS | Max(udS-X,0) | Max(X-udS,0) |
| Down | Up | duS | Max(duS-X,0) | Max(X-duS,0) |
| Down | Down | ddS | Max(ddS-X,0) | Max(dds-X,0) |
Example
You have an American call option expiring in 2-years with exercise price of $30 on a stock which currently trades at $34. You expect the stock to increase by a factor of 1.25 and decrease by a factor of 0.70. If the interest rate is 3%, determine the option value.
We first need to determine the probability of an up movement using the risk-neutral formula:
$$ \pi=\frac{\text{1}+\text{3%}\ -\text{0.7}}{\text{1.25}\ -\ \text{0.7}}=\text{0.6} $$
The following binomial tree summarizes the option valuation at different nodes:
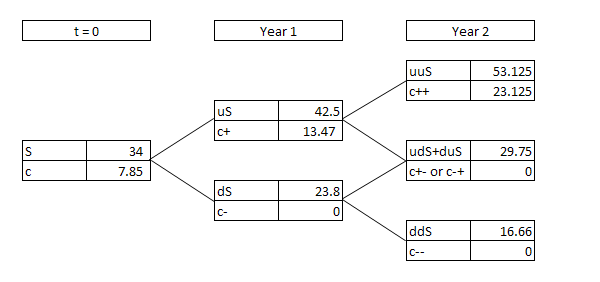
The price of the underlying and the pay-off of the call option, at the end of Year 2, in case of up movement in both Year 1 and Year 2, equals $53.125 (=$34 × 1.25 × 1.25) and $23.125 ($53.125 - $30) respectively.
Similarly, the price of the underlying and associated call option in case of one down and one up movement in either of Year 1 or Year 2 equals $29.75 (=$34 × 1.25 × 0.7) and $0 respectively. The call option value at end of Year 2 in this case is 0 because the spot price is lower than the exercise price. In case of a down movement in both years, the spot price at end of Year 2 will be reduced to $16.66 and the call option will be worthless.
Using these final pay-offs, we can find out the call option value at the end of Year 1. In case of an upward movement in Year 1, there is a probability of 0.6 that the option will be worth $23.125 (corresponding to underlying value of $53.125) and a probability of 0.4 that it will be 0 (corresponding to underlying value of $29.75) at the end of Year 2. This information can be used to find out the option value at the end of Year 1:
$$ \text{c}^+=\frac{\text{0.6}\times\text{\$23.125}+(\text{1}-\text{0.6})\times\text{0}}{\text{1}+\text{3%}}=\text{\$13.47} $$
Using the same approach, we can determine c-, which equals 0.
The option values at end of Year 1, i.e. c+ and c- can be used to determine the option value at time 0, i.e. c:
$$ \text{c}=\frac{\text{0.6}\times\text{\$13.47}+(\text{1}-\text{0.6})\times\text{0}}{\text{1}+\text{3%}}=\text{\$7.85} $$
by Obaidullah Jan, ACA, CFA and last modified on