Average Variable Cost
In economics, average variable cost (AVC) is the variable cost per unit. Variable costs are such cost which vary directly with change in output. AVC equals total variable cost divided by output.
A firm’s composition of variable costs depends on the time period being considered. Firms can change all their inputs, both labor and capital, in the long-run; but in the short-run, at least one of the inputs is fixed. It follows that in the short run, average variable cost is different from average total cost but in the long-run average variable cost and average total cost are effectively the same.
Average variable cost is important because it helps a firm in deciding whether it should continue operating in the short-run. It is feasible to operate only when the marginal revenue is higher than average variable cost.
Formula
Average variable cost is calculated by dividing total variable cost VC by output Q.
$$ \text{AVC}\ =\ \frac{\text{VC}}{\text{Q}} $$
In the short-run, a firms’ costs can be broadly categories into either fixed or variable:
$$ \text{TC}\ =\ \text{FC}\ +\ \text{VC} $$
This can be converted to per-unit form by dividing both sides by Q:
$$ \frac{\text{TC}}{\text{Q}}\ =\ \frac{\text{FC}}{\text{Q}}\ +\ \frac{\text{VC}}{\text{Q}} $$
TC/Q equals average total cost (ATC), FC/Q equals average fixed cost (AFC) and VC/Q equals average variable cost (AVC):
$$ \text{ATC}\ =\text{AFC}\ +\ \text{AVC} $$
$$ \text{AVC} =\text{ATC} - \text{AFC} $$
This gives us another definition of the short-run average variable cost. AVC equals ATC minus AFC.
Average variable cost can be worked out directly from a firm’s cost function. We need to subtract the fixed cost and then divide by Q. Let’s consider a firm whose total cost function is given as follows:
$$ \text{TC}\ =\ \text{0.1Q}^\text{3}-\ \text{2Q}^\text{2}+\text{60Q}+\text{200}\ $$
We can convert this total cost function to a function for average variable cost as follows:
$$ \text{AVC}\ =\ \frac{\text{TC}\ -\ \text{FC}}{\text{Q}} $$
$$ \text{AVC}\ =\ \frac{\text{0.1Q}^\text{3}-\ \text{2Q}^\text{2}+\text{60Q}+\text{200}\ -\ \text{200}}{\text{Q}} $$
$$ \text{AVC}\ =\ \text{0.1Q}^\text{2}-\ \text{2Q}+\text{60} $$
If we plot the average variable cost function, we get a U-shaped cost-curve shown below:
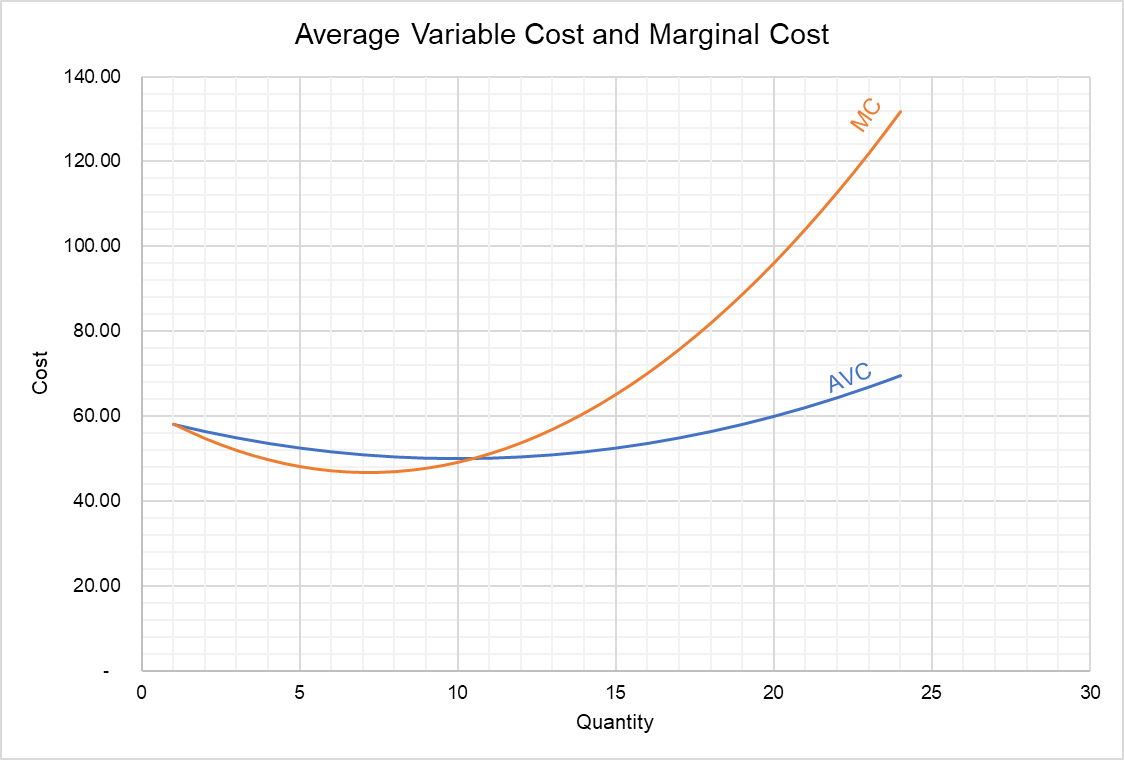
You can see that the average variable cost curve is U-shaped. It initially declines but ultimately it starts rising. It declines because marginal product initially rises but eventually starts rising because at least one input, typically capital, is fixed in the short-run and in presence of a fixed input, law of diminishing returns govern the marginal product of other factors, such as labor.
Marginal Cost and AVC
Marginal cost is the incremental cost of each additional unit of a product. The cumulative marginal cost of Q units equals total variable cost. Hence, average variable cost effectively equals cumulative marginal cost of Q units divided by Q.
This relationship between marginal cost and AVC can be used to predict the interplay of marginal cost and average variable cost curves.
- If the marginal cost curve is below the average variable cost curve, average variable cost should decline. It is because AVC is the average marginal cost and a marginal cost lower than AVC causes it to decline. On the other hand, if the marginal cost curve is above the average variable cost curve, the average variable cost increases.
- The marginal cost equals average variable cost when the average variable cost is at its minimum.
by Obaidullah Jan, ACA, CFA and last modified on