Profit Maximization
Profit maximization rule (also called optimal output rule) specifies that a firm can maximize its economic profit by producing at an output level at which its marginal revenue is equal to its marginal cost.
Marginal revenue is the change in revenue that results from a change in a change in output. For example, if a firm sells 99 units for $198 and 100 units for $200, marginal revenue of the 100th unit is $2. If ∆TR is the change in total revenue and ∆q is the change in output, MR equals ∆TR/∆q.
Marginal cost, on the other hand, is the incremental cost of additional units of output. For example, if total cost of 99 units is $148.5 and total cost of 100 units is $150, the marginal cost of the 100th units is $1.5. If ∆TC is change in total cost and ∆q is the change in output, MC equals ∆TC/∆q.
It makes intuitive sense that a firm should continue increasing its production as long as marginal revenue is higher than marginal cost because each additional sale increases profit by $0.5 ($2 minus $1.5). But if the marginal cost is higher than the marginal revenue, it means that the firm is spending more money on the unit than it earns, and it doesn’t make sense to produce it. It follow that if MR is greater than MC, a firm should increase production and if MR is less than MC, it should decrease production. The only point at which a firm doesn’t need to do anything to reach profit-maximization is the one at which MR=MC.
Why MR = MC is Profit-Maximizing?
We can arrive at the same conclusion algebraically. A firm’s profit (π) equals its total revenue (TR) minus its total cost (TC):
$$ \pi=\text{TR}\ - \text{TC} $$
This expression can be written as follows:
$$ \frac{\Delta �\text{�}}{\Delta \text{q}}=\frac{\Delta \text{TR}}{\Delta \text{q}} - \frac{\Delta \text{TC}}{\Delta \text{q}} $$
It means that the rate of change of profit equals the difference between the rate of change of revenue and rate of change of cost.
Now, at the profit-maximizing output, rate of change of profit should be 0 because we have reached the peak of the profit curve. The rate of change in profit was positive till we reached the peak and it would turn negative if we move over it. Hence, it follows that profit maximization is possible if ∆π/∆q is 0.
$$ \text{0}=\frac{\Delta \text{TR}}{\Delta \text{q}} - \frac{\Delta \text{TC}}{\Delta \text{q}} $$
But ∆TR/∆q is the definition of marginal revenue (MR) and ∆TC/∆q is the definition of marginal cost.
$$ \text{0}=\text{MR}\ - \text{MC} $$
$$ \text{MR}=\text{MC} $$
The beauty of MR = MC as the profit maximization point is that it applies to all firms, both in perfect competition or monopoly.
Example
Let’s consider a firm whose total revenue, total cost, marginal revenue and marginal cost functions are given below:
$$ \text{TR}\ =\ \text{90Q}\ -\ \text{2Q}^\text{2} $$
$$ \text{MR}\ =\ \text{90}\ -\ \text{4Q} $$
$$ \text{TC}\ =\ \text{200}\ +\ \text{10Q}+\text{2Q}^\text{2} $$
$$ \text{MC}\ =\ \text{4Q}\ +\ \text{10} $$
We can find the profit-maximizing output using the MR = MC condition:
$$ \text{MR}\ =\ \text{MC} $$
$$ \text{MR}\ =\ \text{90}\ -\ \text{4Q}\ =\ \text{MC}\ =\ \text{4Q}\ +\ \text{10} $$
$$ \text{Q}\ =\ \text{10} $$
The profit-maximizing output can also be determined from the intersection of marginal revenue and marginal cost curves.
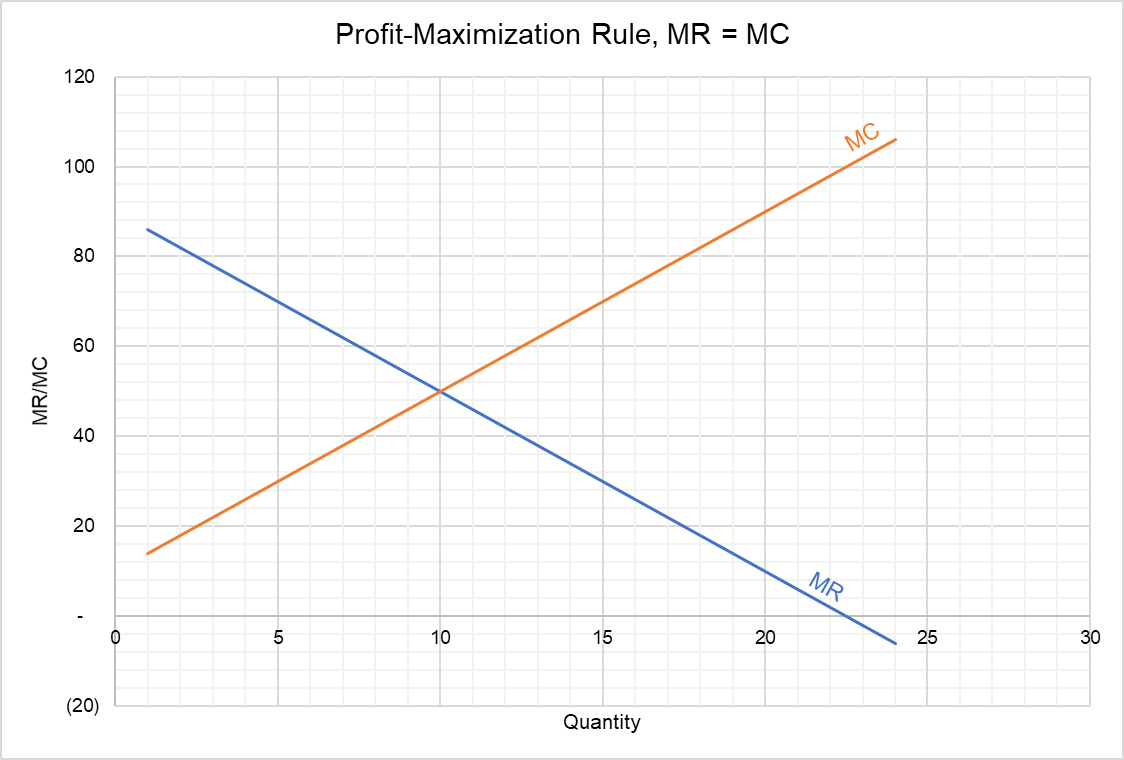
The total revenue and total cost graph shows that 10 units are indeed the profit-maximizing output because the distance between the total revenue curve and total cost curve is maximum at 10 units.

by Obaidullah Jan, ACA, CFA and last modified on