Excel IRR Function
IRR is an Excel function that calculates the internal rate of return where the cash flows occur at the end of each period of equal duration. Internal rate of return (IRR) is a capital budgeting tool which works out the rate at which the present value of a project’s net cash flows equals its initial investment outlay. Only projects whose internal rate of return is greater than the risk-adjusted required rate of return, should be considered for investment.
IRR, XIRR and MIRR are three Excel functions associated with internal rate of return. IRR function is the most basic and straight forward: it calculates internal rate of return assuming that (a) cash flows occur at the end of each period, (b) there is equal time between two cash flows and (c) cash flows that are generated by project can be reinvested at the internal rate of return.
IRR is an iterative function, i.e. Excel tries different values until it reaches a value that fits the following equation:
$$ \text{Initial Investment}=\ \frac{\text{CF1}}{{(\text{1}+\text{IRR})}^\text{1}}+\frac{\text{CF2}}{{(\text{1}+\text{IRR})}^\text{2}}+\frac{\text{CF3}}{{(\text{1}+\text{IRR})}^\text{3}}+\ldots+\ \frac{\text{CFn}}{\left(\text{1}+\text{IRR}\right)^\text{n}} $$
CF refers to periodic cash flows and initial investment means total amount invested in the project at t=0
Syntax
IRR syntax is:
IRR(values, [guess])
Values argument refers to the complete stream of project/investment cash flows including the initial investment which must be entered with a negative sign.
[guess] is an optional argument in which we just enter our best assessment of the internal rate of return.
Since Excel uses hit-and-trial method, entering a guess helps Excel to start with the guess value we enter and close in on the best match.
The values we need to enter in the IRR function are the same as required in case of NPV with one major difference. In case of IRR, we need to include the initial investment outlay as part of the values while in case of NPV, we exclude it from NPV and manually subtract it.
Example
The following screenshot shows the difference in which IRR and NPV formulas should be used with a same set of project cash flows stream:
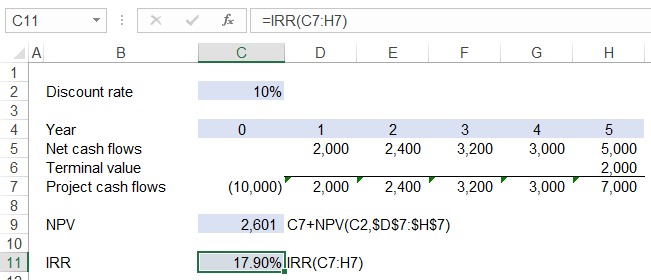
IRR and NPV functions are the most commonly used IRR and NPV functions in Excel because in most cases it is safe to assume cash flows are equally spread-out and occur at the year end, but what if these cash flows weren’t equidistant. In such a situation we turn to XIRR and XNPV functions.
by Obaidullah Jan, ACA, CFA and last modified on