Prisoners' Dilemma
A prisoners’ dilemma refers to a type of economic game in which the Nash equilibrium is such that both players are worse off even though they both select their optimal strategies.
The prisoners’ dilemma is a classic example of a game which involves two suspects, say P and Q, arrested by police and who must decide whether to confess or not. If one confesses but the other doesn’t, the prisoner which confesses gets a lighter prison term, say 1 year, but the prisoner which doesn’t confess get a very harsh term, say 8 years. If neither confesses, they both get lighter terms, say 2 years each; but if both confess, both of them get a strict term, say 4 years each.
The game can be visualized using the following payoff matrix:
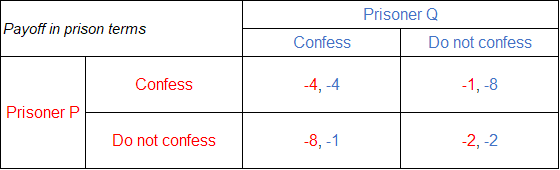
The combined optimal strategy for both prisoners is to not confess. It is because doing so would result in the minimum combined prison term for them. But since they can’t communicate and cooperate, in attempting to do their best individually, they select strategies which doom them both.
Let’s look at the game from the perspective of Prisoner P. If Prisoner Q confesses, it is better for Prisoner P to confess too because otherwise he would get a term of 8 years instead of 4 years. Similarly, if Prisoner Q doesn’t confess, it is in the interest of Prisoner P to confess because by confessing he would get a 1-year term instead of 2 years. Hence, no matter what Prisoner Q does, confessing in the dominant strategy for Prisoner P.
Now, let’s consider the point of view of Prisoner Q. He knows that confessing is the dominant strategy of Prisoner Q. He doesn’t want to not confess and get an 8-year term and confesses. But when he does so, both get 4-year prison terms each. Ultimately both are worse off because they get 4 years each instead of just 2 years each. But they can’t escape this unfortunate outcome because they can’t cooperate, and any other strategy would be worst for each prisoner individually.
Nash Equilibrium in Prisoners’ Dilemma
The outcome of the prisoner’s dilemma is a Nash equilibrium. A Nash equilibrium is a combination of strategies such that player firm has any incentive to unilaterally change its strategy. When both players of a game have dominant strategies, the outcome which is the intersection of the dominant strategies is a Nash equilibrium.
In the prisoners’ dilemma, since confessing is dominant strategy for each prisoner, the Nash equilibrium occurs when both confess. It is Nash equilibrium because no prisoner is better off by unilaterally changing its strategy. For example, if Prisoner P decides to not confess while Prisoner Q does confess, Prisoner P would get 8 years instead of 4 years. Hence, Prisoner P is worse off if he moves away from the Nash equilibrium. He wouldn’t choose a strategy other than the one dictated by the Nash equilibrium. This shows how a Nash equilibrium is self-reinforcing and stable.
Examples
Even though the prisoners’ dilemma discussed above is an abstract concept, many real-life situations closely resemble it. For example:
- Firms know that if they don’t advertise, they can maintain their existing market share and pocket the saved advertising budget as additional profit, but they advertise anyway because each firm fears that if it doesn’t advertise and the other firm does, it would lose market share. Because both firms are having the same fear, both of them advertise, both have lower profits (due to higher advertising expense) and no one gains any market share.
- Firms deciding about whether to hire a lawyer to represent them in arbitration would be collectively better off if they decide to not hire a lawyer. But each firm hires a lawyer out of fear that if the other firm hires a lawyer and they don’t, the likelihood of the other firm winning in arbitration would increase significantly.
- Firms in oligopoly are better off if they could both restrict their output and charge a monopoly price. But since collusion is illegal, both produce a higher output which reduces payoff to each firm. The Cournot model is an illustration of such a prisoners’ dilemma.
by Obaidullah Jan, ACA, CFA and last modified on