Nash Equilibrium
Nash equilibrium is an outcome of a game such that no player can gain by unilaterally changing its strategy. It is achieved when each player adopts the optimal strategy given the strategy of the other player.
Nash equilibrium is named after John Nash, a famous game theorist played by Russel Crow in ‘A Beautiful Mind’.
The most important property of Nash equilibrium is that it is self-enforcing. It is the outcome which two rational players A and B should ultimately reach in a non-cooperative game. Player A reaches Nash equilibrium by employing a strategy which is his best response to the strategy chosen by its opponent, Player B. But since the opponent i.e. Player B also choses a strategy which gives him the maximum payoff given the strategy of Player A, the game gravitates towards an inevitable outcome. This outcome is called a Nash equilibrium.
Even though it is in the best interest of each player to adopt a strategy dictated by the Nash equilibrium, it is not necessary that the Nash equilibrium would maximize the combined payoff. Prisoners’ dilemma is a classic example of this phenomena.
A Nash equilibrium is stable because no player can improve its payoff by changing its strategy.
Nash Equilibrium vs Dominant Strategy
A dominant strategy is a type of Nash equilibrium.
A dominant strategy is a strategy which results in the best payoff for a player no matter what the other firm does but a Nash equilibrium represents a strategy which maximizes payoff given what the other player would do. A Nash equilibrium is conditional upon the other player’s best strategy, but a dominant strategy is unconditional. We reach a Nash equilibrium by assuming that the other player is rational, but we can follow a dominant strategy without forecasting expected strategy of the opponent.
A game has a Nash equilibrium even if there is no dominant strategy (see example below). It is also possible for a game to have multiple Nash equilibria.
Finding Nash Equilibrium
Following rules are useful in identifying a game’s Nash equilibrium.
- If both players have dominant strategies i.e. strategies which get them the best payoff no matter what the other player does, the cell in which the dominant strategies of both players intersect is the Nash equilibrium.
- If one player has a dominant strategy, the cell in the dominant strategy row or column in which the other player has the maximum payoff is the Nash equilibrium.
- If no firm has any dominant strategy, identify any dominated strategies and cross those cell out. Identify the maximum payoffs for each player in each row and column and place check marks against them. Cells in which both payoffs are checked show the potential Nash equilibria.
Example
Let’s consider two firms A and B who must decide about their advertising budget. The following payoff matrix shows net increase in profit of each firm under different scenarios:
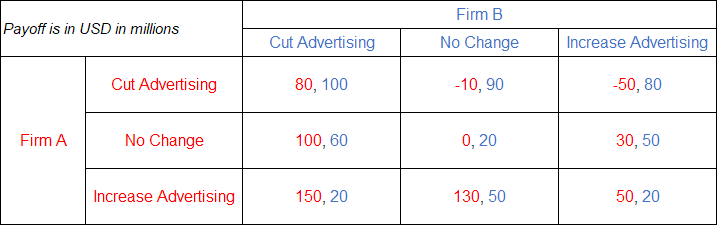
There is a dominant strategy in this game for Firm A i.e. to advertise. It is because the maximum payoff for row player in all columns occurs in the last row.
Firm B has no dominant strategy because its maximum payoff doesn’t occur in the same column. When Firm A cuts its advertising budget, Firm B’s maximum payoff occurs when it also follows. Similarly, when Firm A doesn’t change its advertising budget, Firm B does best by cutting its advertising. But if Firm A increases its advertising spending, Firm B’s best strategy is to not change its current advertising budget.
There is no dominated strategy either for Firm B because there is no column in which its payoff is always worst.
Using the rules discussed above, we know that the Nash equilibrium must exist in the last row i.e. the dominant strategy of Firm A. In other words, Nash equilibrium in this game would occur when Firm A advertises. Give this fact, we need to find which cell gives us the maximum payoff for Firm B in the last row. It is the second column which represents Firm B not changing its advertising budget. Row 3 and Column 2 hence show a Nash equilibrium because:
- Firm A has no incentive to change its strategy because increasing advertising is its dominant strategy.
- Since Firm A will advertise in any case, Firm B’s best response is to not change its budget because this gets it the maximum payoff. If Firm B cuts its advertising budget or increases it, its payoff will drop to $20 million in each case which is worse than $50 million.
by Obaidullah Jan, ACA, CFA and last modified on