Newton Raphson Method
Newton Raphson Method is yet another numerical method to approximate the root of a polynomial. Newton Raphson Method is an open method of root finding which means that it needs a single initial guess to reach the solution instead of narrowing down two initial guesses.
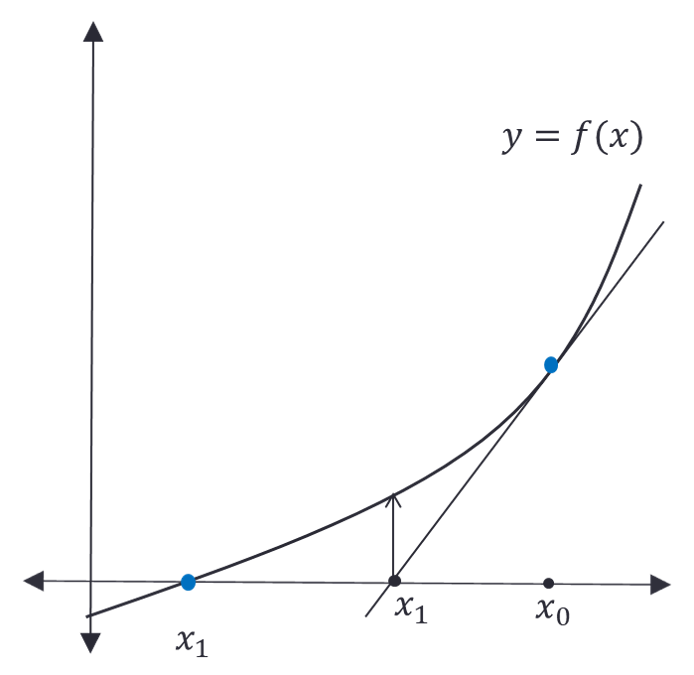
Newton Raphson Method uses to the slope of the function at some point to get closer to the root. Using equation of line y = mx0 + c we can calculate the point where it meets x axis, in a hope that the original function will meet x-axis somewhere near. We can reach the original root if we repeat the same step for the new value of x.
Formula
The following formula gives the next value of x (hopefully closer to the root)
$$ \text{x} _ {\text{n}+\text{1}}=\text{x} _ \text{n}-\frac{\text{f}\left(\text{x} _ \text{n}\right)}{\text{f}^\prime\left(\text{x} _ \text{n}\right)} $$
Steps
- Initial guess
- Using the formula mentioned above calculate the next value of x
- Check if x is the root of the function or is in the range of affoardable error. In other words check if f(x)=0 or |f(x)| < affordable error. Repeat step 2 if not. 3 (option b) If the formula mentioned above gives the same result, x is the root of the polynomial.
Example
Let's approximate the root of the following function with Newton Raphson Method
$$ \ \text{f}\left(\text{x}\right)\ =\ \text{e}^{-\text{x}}-\text{x} $$
Solution
$$ \text{f}\left(\text{x}\right)=\text{e}^{-\text{x}}-\text{x} $$
show hidden steps
$$ \frac{\text{df}}{\text{dx}}=-\text{e}^{-\text{x}}-\text{1} $$
$$ \text{x} _ {\text{n}+\text{1}}=\text{x} _ \text{n}-\frac{\text{f}\left(\text{x} _ \text{n}\right)}{\text{f}^\prime\left(\text{x} _ \text{n}\right)}=\text{x} _ \text{n}+\frac{\text{e}^{-\text{x} _ \text{n}}-\text{x} _ \text{n}}{\text{e}^{-\text{x} _ \text{n}}+\text{1}\mathrm{\ } } $$
$$ \text{error} < \text{0.05%} $$
$$ \text{x} _ {\text{n}+\text{1}}=\text{x} _ \text{n}+\frac{\text{e}^{-\text{x} _ \text{n}}-\text{x} _ \text{n}}{\text{e}^{-\text{x} _ \text{n}}+\text{1}\mathrm{\ } } $$
| xn | xn+1 | error | |
|---|---|---|---|
| 1 | 0 | 0.5 | |
| 2 | 0.5 | 0.5663 | |
| 3 | 0.5663 | 0.5671 | 0.0014 |
| 4 | 0.5671 | 0.5671 | 0.0000 |
The relative error is 0 because we have found the exact root and a function.
by Arifullah Jan and last modified on